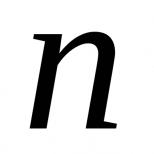Собственные числа и вектора. Матрицы и векторы. записать каноническое разложение матрицы
Введение………………………………………………………………………..3
Суть метода прогонки…………………………………………………..4
Теоретическая часть. ................................................................................5
Виды прогонки…………………………………………………………..7
Теорема о корректности и устойчивости прогонки…………………..10
Решение системы методом прогонки. Код, реализующий метод прогонки…………………………………………………………………..12
Трёхдиагональная матрица (матрица Якоби)…………………………15
Заключение……………………………………………………………………..19
Список литературы…………………………………………………………….20
ВВЕДЕНИЕ
Прогонкой называется модификация метода Гаусса для решения систем линейных алгебраических уравнений с трехдиагональной матрицей. Если матрица системы обладает определенными свойствами, то метод прогонки является численно устойчивым и очень эффективным методом, который позволяет практически мгновенно решать одномерные краевые задачи, одну из которых мы рассмотрели в предыдущем разделе. Большинство корректно поставленных физических задач приводит к системе уравнений с хорошей матрицей, и в этих случаях метод прогонки проявляет слабую чувствительность как к погрешностям задания начальных условий, так и к погрешностям вычислительного характера.
1. Суть метода прогонки
Суть метода прогонки заключается в том, что, используя специфику структуры матрицы системы уравнений (наличие трех диагоналей), удается получить рекуррентные формулы для вычисления последовательности коэффициентов прогонки, которые позволяют на обратном ходу вычислить значения функции в узлах сетки. Рассматривая конечно-разностное уравнение для первой тройки узлов:
b1U1+c1U2=-a1U0,
видим, что оно связывает между собой два соседних значения U1, и U 2 . Перепишем его в виде:
d1U2+e=U1, (1)
где d 1 и е1вычисляются по известным значениям. Наблюдательный читатель заметит, что это справедливо только для задач первого рода. Чуть позже мы получим общее решение. Теперь мы можем исключить £/, из уравнения для следующей тройки узлов:
a2U1+b2U2+c2U2=f2,
подставив значение U1 из уравнения (8). После этой процедуры последнее уравнение также может быть приведено к виду:
d3U3+e2=U2,
di-1Ui+ei-1=Ui-1,
в уравнение
aiUi-1+biUi+ciUi+1=fi,
Ui=-+ (2)
Это соотношение дает две рекуррентные формулы для коэффициентов:
di=-Ci/(ai*di-1+bi) (3)
ei=(fi-ai*ei-1)/(aidi-1+bi) (4)
Цикл вычисления последовательности коэффициентов в соответствии с этими формулами носит название прямого хода прогонки.
do=yo , eo=бo,
Цикл прямого хода повторяется N-1 раз. Последними будут вычислены коэффициенты d N-1 и e N-1 , которые связывают функции в двух узлах вблизи правой границы:
Un-1=dn-1Un+en-1 (5)
Если на правой границе задано условие первого рода U n = с, то уже можно вычислить U n-1 и далее продолжать обратный ход прогонки при I = N - 1,..., 1, 0. Если условие более сложное, то надо рассмотреть уравнение (6), определяющее граничное условие на правой границе. Напомним его:
Un=ynUn-1+бn (6)
Соотношения (6) и (5) составляют систему из двух уравнений с двумя неизвестными. Используя определители, запишем ее решение.
Un-1=(en-1+бndn-1)/(1-yndn-1) (7)
Un=(бn+ynen-1)/(1-yndn-1)
Таким образом, мы нашли значения в двух узлах, лежащих вблизи правой границы расчетной области. Теперь, используя формулу (2) и уменьшая индекс i от N= 2 до 0, можно вычислить все неизвестные £/.. Этот процесс носит название обратного хода прогонки. Почему-то в голову приходит лозунг нашего времени: «Цели ясны, задачи определены.
2. Теоретическая часть
Пусть Ax=b, где A – трехдиагональная матрица. Матрица A= называется (2m+1) – диагональной, если a ij =0 при |i-j|>m.
Для решения систем уравнений такого вида часто наиболее целесообразно применять метод Гаусса при естественном порядке исключения неизвестных. В случае, когда этот метод применяется для решения СЛАУ, его называют методом прогонки .
Получаем , используем метод прогонки, исходя из следующего рекуррентного соотношения:,(2) получаем:

Эти формулы представляют собой прямой проход метода. Обратный проход:

Остальные x i находим из формулы (2).
Для применимости метода прогонки достаточно, чтобы матрица A была с диагональным преобладанием.
Алгоритм:
1. Вводим str/stlb – количество строк/столбцов, A – элементы расширенной матрицы
2. Проверяем матрицу на диагональное преобладание
3. Если матрица с диагональным преобладанием тогда п.4, иначе п.8
4. Выполняем прямой ход метода (формулы (3), (4)): c:=A/A; d:=A/A;
c[i]:= (-A)/(A*c+A);
d[i]:= (A-A*d)/(A*c+A)
x:=(A-A*d)/(A+A*c);
x[i]:=c[i]*x+d[i];
6. Выводим x;
7. Проверки на невязку;
8. Заканчиваем алгоритм.
В программе : A = B i , A = C i , A = A i , A = b i , d[i] = ? i , c[i] = ? i , str = n.
Описание входной информации: Str (Stlb) – количество строк (столбцов) в расширенной матрице, A – матрица A (i – строки, j – столбцы)
3. Виды прогонки
Часто возникает необходимость в решении линейных алгебраических систем, матрицы которых, являясь слабо заполненными, т.е. содержащими немного ненулевых элементов, имеют определённую структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов метод Гаусса можно трансформировать в более эффективные методы.
Рассмотрим наиболее простой случай ленточных систем , к которым, как увидим впоследствии, сводится решение задач сплайн-интерполяции функций, дискретизации краевых задач для дифференциальных уравнений методами конечных разностей, конечных элементов и др. А именно, будем искать решение такой системы, каждое уравнение которой связывает три “соседних” неизвестных:
b i x i -1 + c i x i + d i x i = r i (1)
где i =1,2 ,...,n ; b 1 = 0, d n = 0. Такие уравнения называются трехточечными разностными уравнениями второго порядка . Система (1) имеет трёхдиагональную структуру, что хорошо видно из следующего, эквивалентного (1), векторно-матричного представления:
c 1 d 1 0 0 ... 0 0 0 x 1 r 1
b 2 c 2 d 2 0 ... 0 0 0 x 2 r 2
0 b 3 c 3 d 3 ... 0 0 0 x 3 r 3
. . . . ... . . . * ... = ...
0 0 0 0 ... b n -1 c n -1 d n -1 x n -1 r n-1
0 0 0 0 ... 0 b n c n x n r n
Как и в решении СЛАУ методом Гаусса, цель избавится от ненулевых элементов в поддиаганальной части матрицы системы, предположим, что существуют такие наборы чисел δ i и λ i (i =1,2 ,...,n ) , при которых
x i = δ i x i+1 + λ i (2)
т.е. трехточечное уравнение второго порядка (1) преобразуется в двухточечное уравнение первого порядка (2). Уменьшим в связи (2) индекс на единицу и полученое выражение x i -1 = δ i -1 x i + λ i -1 подставим в данное уравнение (1):
b i δ i-1 x i + b i λ i-1 + c i x i + d i x i+1 = r i
x i = - ((d i /( c i + b i δ i-1 )) x i-1 + (r i - b i λ i-1 )/( c i - b i δ i-1 )).
Последнее равенство имеет вид (2) и будет точно с ним совпадать, иначе говоря, представление (2) будет иметь место, если при всех i =1,2,…, n выполняются рекуррентные соотношения
δ i = - d i /( c i + b i δ i-1 ) , λ i = (r i - b i λ i-1 )/( c i - b i δ i-1 ) (3)
Легко видеть, что, в силу условия b 1 =0 , процесс вычисления δ i , λ i может быть начат со значений
δ 1 = - d 1 / c 1 , λ 1 = r 1 / c 1
и продолжен далее по формулам (3) последовательно при i =2,3,..., n , причем при i = n , в силу d n =0, получим δ n = 0.Следовательно, полагая в (2) i = n ,будем иметь
x n = λ n = (r n – b n λ n-1 )/( c n – b n δ n-1 )
(где λ n -1 , δ n -1 – уже известные с предыдущего шага числа). Далее по формулам (2) последовательно находятся x n -1 , x n -2 ,…, x 1 при i = n -1, n -2,...,1 соответственно.
Таким образом, решение уравнений вида (1) описываем способом, называемым методом прогонки , сводится к вычислениям по трём простым формулам: нахождение так называемых прогоночных коэффициентов δ i , λ i по формулам (3) при i =1,2,…, n (прямая прогонка ) и затем неизвестных x i по формуле (2) при i = n -1, n -2,...,1 (обратная прогонка ).
Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при больших размерностях систем не должно быть строгого роста погрешностей округлений.
Будем называть прогонку корректной , если знаменатели прогоночных коэффициентов (3) не обращаются в нуль, и устойчивой , если |δ i |< 1 при всех i € {1,2, ..., n }.
Приведем простые достаточные условия корректности и устойчивости прогонки, которые во многих приложениях метода автоматически выполняются.
Назначение . Данный сервис предназначен для решения задач динамического программирования методами прямой и обратной прогонки в онлайн режиме (см. пример решения задачи оптимального распределения инвестиций).Инструкция . Выберите количество объектов и количество групп возможных вариантов, нажмите Далее. В новом окне выберите метод прогонки .
Пример №1 . Решить задачу методом динамического программирования в прямом и обратном времени для целевой функции, заданной таблично.F(x 1 ,x 2 ,x 3) = f 1 (x 1) + f 2 (x 2) + f 3 (x 3) → max
x 1 + 2x 2 + 2x 3 ≤ 5
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| f 1 (x 1) | 6 | 7 | 11 | 12 | 15 | 16 |
| f 2 (x 2) | 9 | 11 | 13 | 15 | ||
| f 3 (x 3) | 8 | 12 | 14 | 16 |
I этап. Условная оптимизация . f 1 (L) = max(f 1); 0 ≤ x 1 ≤ 5; x 1 = 0,1,2,3,4,5.
f 1 (0) = max = 6
f 1 (1) = max = 7
f 1 (2) = max = 11
f 1 (3) = max = 12
f 1 (4) = max = 15
f 1 (5) = max = 16
Таблица 1 – Расчет значения функции f 1 (L)
| L | 0 | 1 | 2 | 3 | 4 | 5 |
| f 1 (L) | 6 | 7 | 11 | 12 | 15 | 16 |
| x 1 | 0 | 1 | 2 | 3 | 4 | 5 |
f 2 (0) = max = 15
f 2 (1) = max = 16
f 2 (2) = max = 20
f 2 (3) = max = 21
f 2 (4) = max = 24
f 2 (5) = max = 25
Таблица 2 – Расчет значения функции f 2 (L)
| L | 0 | 1 | 2 | 3 | 4 | 5 |
| f 2 (L) | 15 | 16 | 20 | 21 | 24 | 25 |
| x 2 | 0 | 0 | 0 | 0 | 0 | 0 |
f 3 (0) = max = 23
f 3 (1) = max = 24
f 3 (2) = max = 28
f 3 (3) = max = 29
f 3 (4) = max = 32
f 3 (5) = max = 33
Таблица 3 – Расчет значения функции f 3 (L)
| L | 0 | 1 | 2 | 3 | 4 | 5 |
| f 3 (L) | 23 | 24 | 28 | 29 | 32 | 33 |
| x 3 | 0 | 0 | 0 | 0 | 0 | 0 |
II этап. Безусловная оптимизация
.
Таким образом, максимум f 3 (5) = 33
При этом x 3 = 0, так как f 3 (5) = 33 достигается при х 3 =0 (см. таблицу 3).
Остальные x распределяются следующим образом:
L = 5 - 2 * 0 = 5
f 2 (5) = 25 достигается при х 2 = 0 (см. таблицу 2).
L = 5 - 2 * 0 = 5
f 1 (5) = 16 достигается при х 1 = 5 (см. таблицу 1).
L = 5 - 1 * 5 = 0
В итоге наилучший вариант достигается при значениях: x 1 = 5, x 2 = 0, x 3 = 0
Пример №2
. Рассмотрим задачу об оптимальном размещении капитала K = nh в m различных независимых фондах (банки, организации, фирма и т.д.), для которых известна ожидаемая прибыль f i при капиталовложениях x i = ih, i = 1..n. Здесь n – количество дискретных приращений h (дискрет), на которые разбит капитал К.
Пусть такие данные имеются по четырем (m=4) фондам для h = 1 млн. руб., n = 6
Решение.
I этап. Условная оптимизация.
1-й шаг: k = 4.
Предположим, что все средства в количестве x 4 = 6 отданы 4-у предприятию. В этом случае максимальный доход, как это видно из таблицы 1*, составит 0.56, следовательно:
F 4 (c 4) = g 4 (x 4)
Таблица 1.
| 0 | x 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x 4 | f 0 (x 0) / F 4 (x 4) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0 |
| 2 | 0.33 | 0 | 0 | 0 | 0 | 0.33 | 0 | 0 |
| 3 | 0.42 | 0 | 0 | 0 | 0.42 | 0 | 0 | 0 |
| 4 | 0.48 | 0 | 0 | 0.48 | 0 | 0 | 0 | 0 |
| 5 | 0.53 | 0 | 0.53 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0.56 | 0.56* | 0 | 0 | 0 | 0 | 0 | 0 |
| c 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F 0 (c 1) | 0 | 0.2 | 0.33 | 0.42 | 0.48 | 0.53 | 0.56 |
| x 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
F 3 (c 3) = max [ g 3 (x 3) + F 4 (c 3 - x 3)]
Таблица 2.
| 0 | x 2 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x 3 | f 3 (x 3) / F 3 (x 3) | 0 | 0.2 | 0.33 | 0.42 | 0.48 | 0.53 | 0.56 |
| 0 | 0 | 0 | 0.2* | 0.33 | 0.42 | 0.48 | 0.53 | 0.56 |
| 1 | 0.15 | 0.15 | 0.35* | 0.48* | 0.57 | 0.63 | 0.68 | 0 |
| 2 | 0.25 | 0.25 | 0.45 | 0.58 | 0.67 | 0.73 | 0 | 0 |
| 3 | 0.4 | 0.4 | 0.6* | 0.73* | 0.82 | 0 | 0 | 0 |
| 4 | 0.5 | 0.5 | 0.7 | 0.83* | 0 | 0 | 0 | 0 |
| 5 | 0.62 | 0.62 | 0.82 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0.73 | 0.73 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 2*.
| c 2 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F 3 (c 2) | 0 | 0.2 | 0.35 | 0.48 | 0.6 | 0.73 | 0.83 |
| x 2 | 0 | 0 | 1 | 1 | 3 | 3 | 4 |
Определяем оптимальную стратегию при распределении средств между остальными предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
F 2 (c 2) = max [ g 2 (x 2) + F 3 (c 2 - x 2)]
Таблица 3.
| 0 | x 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x 2 | f 4 (x 4) / F 2 (x 2) | 0 | 0.2 | 0.35 | 0.48 | 0.6 | 0.73 | 0.83 |
| 0 | 0 | 0 | 0.2 | 0.35 | 0.48 | 0.6 | 0.73 | 0.83 |
| 1 | 0.25 | 0.25* | 0.45* | 0.6 | 0.73 | 0.85 | 0.98 | 0 |
| 2 | 0.41 | 0.41 | 0.61* | 0.76* | 0.89 | 1.01 | 0 | 0 |
| 3 | 0.55 | 0.55 | 0.75 | 0.9* | 1.03* | 0 | 0 | 0 |
| 4 | 0.65 | 0.65 | 0.85 | 1 | 0 | 0 | 0 | 0 |
| 5 | 0.75 | 0.75 | 0.95 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0.8 | 0.8 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 3*.
| c 3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F 4 (c 3) | 0 | 0.25 | 0.45 | 0.61 | 0.76 | 0.9 | 1.03 |
| x 3 | 0 | 1 | 1 | 2 | 2 | 3 | 3 |
Определяем оптимальную стратегию при распределении средств между остальными предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
F 1 (c 1) = max [ g 1 (x 1) + F 2 (c 1 - x 1)]
Таблица 4.
| 0 | x 4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x 1 | f 5 (x 5) / F 1 (x 1) | 0 | 0.25 | 0.45 | 0.61 | 0.76 | 0.9 | 1.03 |
| 0 | 0 | 0 | 0.25 | 0.45 | 0.61 | 0.76 | 0.9 | 1.03 |
| 1 | 0.28 | 0.28* | 0.53* | 0.73* | 0.89 | 1.04 | 1.18 | 0 |
| 2 | 0.45 | 0.45 | 0.7 | 0.9 | 1.06 | 1.21 | 0 | 0 |
| 3 | 0.65 | 0.65 | 0.9* | 1.1* | 1.26* | 0 | 0 | 0 |
| 4 | 0.78 | 0.78 | 1.03 | 1.23 | 0 | 0 | 0 | 0 |
| 5 | 0.9 | 0.9 | 1.15 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1.02 | 1.02 | 0 | 0 | 0 | 0 | 0 | 0 |
Таблица 4*.
| c 4 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| F 5 (c 4) | 0 | 0.28 | 0.53 | 0.73 | 0.9 | 1.1 | 1.26 |
| x 4 | 0 | 1 | 1 | 1 | 3 | 3 | 3 |
1-й шаг: k = 1.
По данным таблицы 4* максимальный доход при распределении 6 между предприятиями составляет c 1 = 6, F 1 (6) = 1.26. При этом 1-му предприятию нужно выделить x 1 = 3.
2-й шаг: k = 2.
c 2 = c 1 - x 1 = 6 - 3 = 3.
По данным таблицы 3* максимальный доход при распределении 3 между предприятиями составляет c 2 = 3, F 2 (3) = 0.61. При этом 2-му предприятию нужно выделить x 2 = 2.
3-й шаг: k = 3.
Определим величину оставшихся денежных средств, приходящихся на долю остальных предприятий.
c 3 = c 2 - x 2 = 3 - 2 = 1.
По данным таблицы 2* максимальный доход при распределении 1 между предприятиями составляет c 3 = 1, F 3 (1) = 0.2. При этом 3-му предприятию нужно выделить x 3 = 0.
4-й шаг: k = 4.
Определим величину оставшихся денежных средств, приходящихся на долю остальных предприятий.
c 4 = c 3 - x 3 = 1 - 0 = 1.
По данным таблицы 1* максимальный доход при распределении 1 между предприятиями составляет c 4 = 1, F 4 (1) = 0.20. При этом 4-му предприятию нужно выделить x 4 = 1.
Таким образом, оптимальный план инвестирования предприятия:
x 1 = 3
x 2 = 2
x 3 = 0
x 4 = 1
который обеспечит максимальный доход, равный: F(6) = g 1 (3) + g 2 (2) + g 3 (0) + g 4 (1) = 0.65 + 0.41 + 0 + 0.20 = 1.26.
Введение………………………………………………………………………..3
Суть метода прогонки…………………………………………………..4
Теоретическая часть. ................................................................................5
Виды прогонки…………………………………………………………..7
Теорема о корректности и устойчивости прогонки…………………..10
Решение системы методом прогонки. Код, реализующий метод прогонки…………………………………………………………………..12
Трёхдиагональная матрица (матрица Якоби)…………………………15
Заключение……………………………………………………………………..19
Список литературы…………………………………………………………….20
ВВЕДЕНИЕ
Прогонкой называется модификация метода Гаусса для решения систем линейных алгебраических уравнений с трехдиагональной матрицей. Если матрица системы обладает определенными свойствами, то метод прогонки является численно устойчивым и очень эффективным методом, который позволяет практически мгновенно решать одномерные краевые задачи, одну из которых мы рассмотрели в предыдущем разделе. Большинство корректно поставленных физических задач приводит к системе уравнений с хорошей матрицей, и в этих случаях метод прогонки проявляет слабую чувствительность как к погрешностям задания начальных условий, так и к погрешностям вычислительного характера.
1. Суть метода прогонки
Суть метода прогонки заключается в том, что, используя специфику структуры матрицы системы уравнений (наличие трех диагоналей), удается получить рекуррентные формулы для вычисления последовательности коэффициентов прогонки, которые позволяют на обратном ходу вычислить значения функции в узлах сетки. Рассматривая конечно-разностное уравнение для первой тройки узлов:
b1U1+c1U2=-a1U0,
видим, что оно связывает между собой два соседних значения U1, и U 2 . Перепишем его в виде:
d1U2+e=U1, (1)
где d 1 и е1вычисляются по известным значениям. Наблюдательный читатель заметит, что это справедливо только для задач первого рода. Чуть позже мы получим общее решение. Теперь мы можем исключить £/, из уравнения для следующей тройки узлов:
a2U1+b2U2+c2U2=f2,
подставив значение U1 из уравнения (8). После этой процедуры последнее уравнение также может быть приведено к виду:
d3U3+e2=U2,
di-1Ui+ei-1=Ui-1,
в уравнение
aiUi-1+biUi+ciUi+1=fi,
Ui=-+ (2)
Это соотношение дает две рекуррентные формулы для коэффициентов:
di=-Ci/(ai*di-1+bi) (3)
ei=(fi-ai*ei-1)/(aidi-1+bi) (4)
Цикл вычисления последовательности коэффициентов в соответствии с этими формулами носит название прямого хода прогонки.
do=yo , eo=бo,
Цикл прямого хода повторяется N-1 раз. Последними будут вычислены коэффициенты d N-1 и e N-1 , которые связывают функции в двух узлах вблизи правой границы:
Un-1=dn-1Un+en-1 (5)
Если на правой границе задано условие первого рода U n = с, то уже можно вычислить U n-1 и далее продолжать обратный ход прогонки при I = N - 1,..., 1, 0. Если условие более сложное, то надо рассмотреть уравнение (6), определяющее граничное условие на правой границе. Напомним его:
Un=ynUn-1+бn (6)
Соотношения (6) и (5) составляют систему из двух уравнений с двумя неизвестными. Используя определители, запишем ее решение.
Un-1=(en-1+бndn-1)/(1-yndn-1) (7)
Un=(бn+ynen-1)/(1-yndn-1)
Таким образом, мы нашли значения в двух узлах, лежащих вблизи правой границы расчетной области. Теперь, используя формулу (2) и уменьшая индекс i от N= 2 до 0, можно вычислить все неизвестные £/.. Этот процесс носит название обратного хода прогонки. Почему-то в голову приходит лозунг нашего времени: «Цели ясны, задачи определены.
2. Теоретическая часть
Пусть Ax=b, где A – трехдиагональная матрица. Матрица A= называется (2m+1) – диагональной, если a ij =0 при |i-j|>m.
Для решения систем уравнений такого вида часто наиболее целесообразно применять метод Гаусса при естественном порядке исключения неизвестных. В случае, когда этот метод применяется для решения СЛАУ, его называют методом прогонки .
Получаем , используем метод прогонки, исходя из следующего рекуррентного соотношения:,(2) получаем:

Эти формулы представляют собой прямой проход метода. Обратный проход:

Остальные x i находим из формулы (2).
Для применимости метода прогонки достаточно, чтобы матрица A была с диагональным преобладанием.
Алгоритм:
1. Вводим str/stlb – количество строк/столбцов, A – элементы расширенной матрицы
2. Проверяем матрицу на диагональное преобладание
3. Если матрица с диагональным преобладанием тогда п.4, иначе п.8
4. Выполняем прямой ход метода (формулы (3), (4)): c:=A/A; d:=A/A;
c[i]:= (-A)/(A*c+A);
d[i]:= (A-A*d)/(A*c+A)
x:=(A-A*d)/(A+A*c);
x[i]:=c[i]*x+d[i];
6. Выводим x;
7. Проверки на невязку;
8. Заканчиваем алгоритм.
В программе : A = B i , A = C i , A = A i , A = b i , d[i] = ? i , c[i] = ? i , str = n.
Описание входной информации: Str (Stlb) – количество строк (столбцов) в расширенной матрице, A – матрица A (i – строки, j – столбцы)
3. Виды прогонки
Часто возникает необходимость в решении линейных алгебраических систем, матрицы которых, являясь слабо заполненными, т.е. содержащими немного ненулевых элементов, имеют определённую структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов метод Гаусса можно трансформировать в более эффективные методы.
Рассмотрим наиболее простой случай ленточных систем , к которым, как увидим впоследствии, сводится решение задач сплайн-интерполяции функций, дискретизации краевых задач для дифференциальных уравнений методами конечных разностей, конечных элементов и др. А именно, будем искать решение такой системы, каждое уравнение которой связывает три “соседних” неизвестных:
b i x i -1 + c i x i + d i x i = r i (1)
где i =1,2 ,...,n ; b 1 = 0, d n = 0. Такие уравнения называются трехточечными разностными уравнениями второго порядка . Система (1) имеет трёхдиагональную структуру, что хорошо видно из следующего, эквивалентного (1), векторно-матричного представления:
c 1 d 1 0 0 ... 0 0 0 x 1 r 1
b 2 c 2 d 2 0 ... 0 0 0 x 2 r 2
0 b 3 c 3 d 3 ... 0 0 0 x 3 r 3
. . . . ... . . . * ... = ...
0 0 0 0 ... b n -1 c n -1 d n -1 x n -1 r n-1
0 0 0 0 ... 0 b n c n x n r n
Как и в решении СЛАУ методом Гаусса, цель избавится от ненулевых элементов в поддиаганальной части матрицы системы, предположим, что существуют такие наборы чисел δ i и λ i (i =1,2 ,...,n ) , при которых
x i = δ i x i+1 + λ i (2)
т.е. трехточечное уравнение второго порядка (1) преобразуется в двухточечное уравнение первого порядка (2). Уменьшим в связи (2) индекс на единицу и полученое выражение x i -1 = δ i -1 x i + λ i -1 подставим в данное уравнение (1):
b i δ i-1 x i + b i λ i-1 + c i x i + d i x i+1 = r i
x i = - ((d i /( c i + b i δ i-1 )) x i-1 + (r i - b i λ i-1 )/( c i - b i δ i-1 )).
Последнее равенство имеет вид (2) и будет точно с ним совпадать, иначе говоря, представление (2) будет иметь место, если при всех i =1,2,…, n выполняются рекуррентные соотношения
δ i = - d i /( c i + b i δ i-1 ) , λ i = (r i - b i λ i-1 )/( c i - b i δ i-1 ) (3)
Легко видеть, что, в силу условия b 1 =0 , процесс вычисления δ i , λ i может быть начат со значений
δ 1 = - d 1 / c 1 , λ 1 = r 1 / c 1
и продолжен далее по формулам (3) последовательно при i =2,3,..., n , причем при i = n , в силу d n =0, получим δ n = 0.Следовательно, полагая в (2) i = n ,будем иметь
x n = λ n = (r n – b n λ n-1 )/( c n – b n δ n-1 )
(где λ n -1 , δ n -1 – уже известные с предыдущего шага числа). Далее по формулам (2) последовательно находятся x n -1 , x n -2 ,…, x 1 при i = n -1, n -2,...,1 соответственно.
Таким образом, решение уравнений вида (1) описываем способом, называемым методом прогонки , сводится к вычислениям по трём простым формулам: нахождение так называемых прогоночных коэффициентов δ i , λ i по формулам (3) при i =1,2,…, n (прямая прогонка ) и затем неизвестных x i по формуле (2) при i = n -1, n -2,...,1 (обратная прогонка ).
Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при больших размерностях систем не должно быть строгого роста погрешностей округлений.
Будем называть прогонку корректной , если знаменатели прогоночных коэффициентов (3) не обращаются в нуль, и устойчивой , если |δ i |< 1 при всех i € {1,2, ..., n }.
Приведем простые достаточные условия корректности и устойчивости прогонки, которые во многих приложениях метода автоматически выполняются.
4. Теорема о корректности и устойчивости прогонки
Пусть коэффициенты b i и d i уравнения (1) при i =2,3,..., n -1 отличны от нуля и пусть
| c i |>| b i |+| d i | i =1,2,…, n . (4)
Тогда прогонка (3), (2) корректна и устойчива (т.е. с i + b i δ i -1 ≠ 0, |δ i |< 1).
Доказательство . Воспользуемся методом математической индукции для установления обоих нужных неравенств одновременно.
При i = 1, в силу (4), имеем:
| c 1 |>| d 1 |≥ 0
Неравенство нулю первой пары прогоночных коэффициентов, а так же
|δ 1 |=|- d 1 / c 1 |< 1
Предположим, что знаменатель (i -1)-x прогоночных коэффициентов не равен нулю и что |δ i -1 |< 1. Тогда, используя свойства модулей, условия теоремы и индукционные предположения, получаем:
|с i + b i δ i -1 |≥| c i | - | b i δ i -1 |>| b i |+| d i | - | bi |*| δi -1 |= | d i |+| bi | (1 - | δ i -1 |)> | d i | >0
а с учетом этого
|δ i |=|- d i / с i +b i δ i-1 |=| δ i |/| с i +b i δ i-1 |< |δ i |/ |δ i |= 1
Следовательно, с i + b i δ i -1 ≠ 0 и |δ i |< 1 при всех i € {1,2, ..., n }, т.е. имеет место утверждаемая в данных условиях корректность и устойчивость прогонки. Теорема доказана.
Пусть А – матрица коэффициентов данной системы (1), удовлетворяющих условиям теоремы, и пусть
δ 1 = - d 1 / c 1 , δ i =|- d i / c i +b i δ i-1 (i=2,3,...,n -1 ), δ n =0
Прогоночные коэффициенты, определяемые первой из формул (3), а
∆ i = с i + b i δ i -1 (i =2,3,..., n )
Знаменатели этих коэффициентов (отличные от нуля согласно утверждению теоремы). Непосредственной проверкой легко убедится, что имеет место представление A = LU , где
c 1 0 0 0 ... 0 0 0
b 2 ∆ 2 0 0 ... 0 0 0
L = 0 b 3 ∆ 3 0 ... 0 0 0
…………………………
0 0 0 0 ... b n -1 ∆ n -1 0
0 0 0 0 ... 0 b n ∆ n
1 -δ 1 0 0 ... 0 0 0
0 1 δ 2 0 ... 0 0 0
U = 0 0 1 δ 3 ... 0 0 0
…………………………
0 0 0 0 ... 0 1 -δ n-1
0 0 0 0 ... 0 0 1
Единственное в силу утверждение теоремы LU -разложения матриц. Как видим, LU-разложение трехдиагональной матрицы А может быть выполнено очень простым алгоритмом, вычисляющем ∆ i δ i при возрастающих значениях i . При необходимости попутно может быть вычислен
det A = c 1 ∏ ∆ i .
В заключение этого пункта заметим, что, во-первых, имеются более слабые условия корректности и устойчивости прогонки, чем требуется в теореме условие строгого диагонального преобладания в матрице А . Во-вторых, применяется ряд других, отличных от рассмотрения нами правой прогонки, методов подобного типа, решающих как поставленную здесь задачу (1) для систем с трехдиагональными матрицами (левая прогонка, встречная прогонка, немонотонная, циклическая, ортогональная прогонки и т.д.), так и для более сложных систем с матрицами ленточной структуры или блочно-матричной структуры (например, матричная прогонка).
5. Решение системы методом прогонки. Код, реализующий метод прогонки
Часто при решении задач математической физики встречаются матрицы, в которых большинство элементов равно нулю. Причем структура матрицы не хаотична, а вполне определена, а именно - матрица трехдиагональна, ненулевые элементы расположены на главной диагонали и двух прилегающих к ней.
Метод прогонки является частным случаем метода Гаусса, и также состоит из прямого и обратного хода. Для решения системы, матрицу сначала нужно привести к двухдиагональной:

Поделив первую строку матрицы, приведенной выше, на -b 1 очевидно, что:

и можно вывести формулу для прямого хода:
Затем необходимо выполнить обратный ход - найти вектор X, из последней строки преобразованной матрицы следует, что x n = Q n .
В тоже время остальные элементы вектора считаются по формуле:
Следует заметить, что метод устойчив если(следует из диагонального преобладания матрицы А):
![]()
и корректен, если(иначе формулы прямого хода не имеют смысла):
![]()
Ниже представлен код, реализующий метод прогонки, принимает трехдиагональную матрицу a размерности N*N, и вектор правых частей b размерности N, результат возвращается в b:
void sweep(double a[N][N],double b[N])
for(i=1;i < N-1;i++)
znam=-a[i][i]-a[i]*a[i]; //общий знаменатель для формул нахождения Pi, Qi
a[i]/=znam; //P i
b[i]=(a[i]*b-b[i])/znam; //Q i
//строка ниже для вычисления Q N
b=(a*b-b)/(-a-a*a);
//обратный ход
for(i=N-2;i > -1;i--)
b[i]+=b*a[i];
Метод прогонки. Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:

Преобразуем первое уравнение системы к виду , где ,
Подставим
полученное выражение во второе уравнение
системы и преобразуем его к виду
и
т.д. На i
-ом
шаге уравнение преобразуется к виду
,
где
![]() ,
.
На m
-ом шаге
подстановка в последнее уравнение
выражения
,
.
На m
-ом шаге
подстановка в последнее уравнение
выражения
![]() дает
возможность определить значение
:
дает
возможность определить значение
:
Значения остальных неизвестных находятся по формулам: , i = m-1, m-2, ..., 1.
Пример 4 . Решение системы уравнений методом прогонки.

Прямой ход прогонки . Вычислим прогоночные коэффициенты:
,
![]() ,
,
![]()
Обратный ход прогонки. Находим значения неизвестных:
,
![]() ,
,
,
,
![]()
Прямые (или точные) методы, позволяют найти решение за определённое количество шагов. Итерационные методы, основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
6. Трёхдиагональная матрица (матрица Якоби)
Трёхдиагональной матрицей или матрицей Якоби называют матрицу следующего вида:
 .
.
Системы линейных алгебраических уравнений с такими матрицами встречаются при решении многих задач математики и физики. Краевые условия x 1 и x n , которые берутся из контекста задачи, задают первую и последнюю строки. Так краевое условие первого рода F (x = x 1) = F 1 определит первую строку в виде C 1 = 1, B 1 = 0, а условие второго рода dF / dx (x = x 1) = F 1 будет соответствовать значениям C 1 = − 1, B 1 = 1.
Метод прогонки
Для решения систем вида или, что то же самое,
используется метод прогонки , основанный на предположении, что искомые неизвестные связаны рекуррентным соотношением:
Используя это соотношение, выразим x i-1 и x i через x i+1 и подставим в уравнение (1):
где F i - правая часть i -го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать

Отсюда следует:
![]()
![]()
Из первого уравнения получим:
После нахождения прогоночных коэффициентов α и β, используя уравнение (2), получим решение системы. При этом,
![]()
Другим способом объяснения существа метода прогонки, более близким к терминологии конечно-разностных методов и объясняющим происхождение его названия, является следующий: преобразуем уравнение (1) к эквивалентному ему уравнению
c надиагональной матрицей
 .
.
Вычисления проводятся в два этапа. На первом этапе вычисляются компоненты матрицы и вектора , начиная с до
![]()
![]()
На втором этапе, для вычисляется решение:
![]()
Такая схема вычисления объясняет также английский термин этого метода «shuttle».
Для применимости формул метода прогонки достаточно свойства диагонального преобладания у матрицы A .
Описание выходной информации: x – матрица-ответ
Заключение
Таким образом, мы:
научились решать системы линейных алгебраических уравнений методом прогонки.
реализовали программный код
доказали теорему о корректности и устойчивости прогонки
рассмотрели на примере решение СЛАУ методом прогонки.
Список литературы
В.М. Вержбитский «Численные методы. Линейная алгебра и нелинейные уравнения», Москава «Высшая школа 2000».
Федеральное агентство по образованию
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Читинский Государственный Университет»
(ЧитГУ)
Энергетический институт
Кафедра прикладной информатики и математики
РЕФЕРАТ
По дисциплине: Численные методы
Тема: Метод прогонки
Выполнил: студентка группы ПИ-08
Цыренжапова Е.В.
Проверил: Станкова М.Г.
#���#####################################################5#=#O###n##########################�X##�###�X##�##8�X##�##T�X##�##p�X##�##x�X##�##��X##�##��X##�###X##�Метод прогонки является модификацией метода Гаусса для частного случая разреженных систем – системы уравнений с трехдиагоналъной матрицей. Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений.
Запишем систему уравнений в виде
На главной диагонали матрицы этой системы стоят элементы b 1, b 2, …, bn ,над ней – элементы с 1, с2,... , с n -1 под ней – элементы а 2, а 3,... , ап (при этом обычно все коэффициенты bi не равны нулю). Остальные элементы матрицы равны нулю.
Метод прогонки состоит из двух этапов – прямой прогонки (аналога прямого хода метода Гаусса) и обратной прогонки (аналога обратного хода метода Гаусса). Прямая прогонка состоит в вычислении прогоночных коэффициентов Ai ,Bi ,с помощью которых каждое неизвестное xi выражается через zi +1 :
Из первого уравнения системы (2.13) найдем
![]()
С другой стороны, по формуле (2.14) Приравнивая коэффициенты в обоих выражениях для х 1, получаем
![]() (2.15)
(2.15)
Подставим во второе уравнение системы (2.13) вместо х 1его выражение через х 2по формуле (2.14):
Выразим отсюда х 2 через х 3:
![]()

Аналогично вычисляют прогоночные коэффициенты для любого номера i :
 (2.16)
(2.16)
Обратная прогонка состоит в последовательном вычислении неизвестных xi . Сначала нужно найти хп. Для этого воспользуемся выражением (2.14) при i = п –1 и последним уравнением системы (2.13). Запишем их:

Отсюда, исключая х n-1 , находим

Далее, используя формулы (2.14) и вычисленные ранее по формулам (2.15), (2.16) прогоночные коэффициенты, последовательно вычисляем все неизвестные х n - 1, xn -2 ,....,х 1. Алгоритм решения системы линейных уравнений вида (2.13) методом прогонки приведен на рис. 2.4.

Рис. 2.4. Алгоритм метода прогонки
При анализе алгоритма метода прогонки надо учитывать возможность деления на нуль в формулах (2.15), (2.16). Можно показать, что при выполнении условия преобладания диагональных элементов, т.е. если , причем хотя бы для одного значения i имеет место строгое неравенство, деления на нуль не возникает, и система (2.13) имеет единственное решение.
Приведенное условие преобладания диагональных элементов обеспечивает также устойчивость метода прогонки относительно погрешностей округлений. Последнее обстоятельство позволяет использовать метод прогонки для решения больших систем уравнений. Заметим, что данное условие устойчивости прогонки является достаточным, но не необходимым. В ряде случаев для хорошо обусловленных систем вида (2.13) метод прогонки оказывается устойчивым даже при нарушении условия преобладания диагональных элементов.
". В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части - факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls , которая сопровождает этот документ.
Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.
Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x (a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2) = x (C 1)+ x (C 2). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера - хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии - это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 ,...., x n , характеризующих набор концентраций C 1 ,C 2 , ..., C m веществ, присутствующих в изучаемой системе.
Рис. 1 Спектры
Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на , где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый (x 1) и второй (x 2) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?
Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.
1. Базовые сведения
1.1 Матрицы
Матрицей называется прямоугольная таблица чисел, например

Рис. 2 Матрица
Матрицы обозначаются заглавными полужирными буквами (A ), а их элементы - соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй - столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как { a ij , i = 1,..., I ; j = 1,..., J }. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.
Пара чисел I и J называется размерностью матрицы и обознается как I ×J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.
1.2. Простейшие операции с матрицами
Матрицы можно умножать на числа . При этом каждый элемент умножается на это число. Например -

Рис. 3 Умножение матрицы на число
Две матрицы одинаковой размерности можно поэлементно складывать и вычитать . Например,

Рис. 4 Сложение матриц
В результате умножения на число и сложения получается матрица той же размерности.
Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A +O = A , A −A = O и 0A = O .
Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A " или индексом A t . Таким образом, если A = {a ij , i = 1,..., I ; j = 1,...,J }, то A t = {a ji , j = 1,...,J ; i = 1,..., I }. Например

Рис. 5 Транспонирование матрицы
Очевидно, что (A t) t = A , (A +B ) t = A t +B t .
1.3. Умножение матриц
Матрицы можно перемножать , но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I ×K , и матрицы B , размерностью K ×J , называется матрица C , размерностью I ×J , элементами которой являются числа
Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц -

Рис.6 Произведение матриц
Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца (c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B
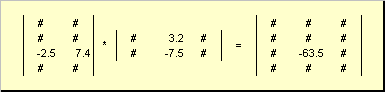
Рис.7 Элемент произведения матриц
Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = (AB )C = A (BC ). Кроме того, оно еще и дистрибутивно, т.е. A (B +C ) = AB +AC . Очевидно, что AO = O .
1.4. Квадратные матрицы
Если число столбцов матрицы равно числу ее строк (I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.
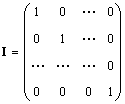
Очевидно AI = IA = A .
Матрица называется диагональной , если все ее элементы, кроме диагональных (a ii ) равны нулю. Например

Рис. 8 Диагональная матрица
Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i >j . Например

Рис. 9 Верхняя треугольная матрица
Аналогично определяется и нижняя треугольная матрица.
Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например

Рис. 10 Симметричная матрица
Матрица A называется ортогональной , если
A t A = AA t = I .
Матрица называется нормальной если
1.5. След и определитель
Следом квадратной матрицы A (обозначается Tr(A ) или Sp(A )) называется сумма ее диагональных элементов,

Например,

Рис. 11 След матрицы
Очевидно, что
Sp(α A ) = α Sp(A ) и
Sp(A +B ) = Sp(A )+ Sp(B ).
Можно показать, что
Sp(A ) = Sp(A t), Sp(I ) = N ,
а также, что
Sp(AB ) = Sp(BA ).
Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det(A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта - матрицы A размерностью (2×2). Тогда
Для матрицы (3×3) определитель будет равен
В случае матрицы (N ×N ) определитель вычисляется как сумма 1·2·3· ... ·N = N ! слагаемых, каждый из которых равен
![]()
Индексы k 1 , k 2 ,..., k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, ... , N ). Вычисление определителя матрицы - это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,

Рис. 12 Определитель матрицы
Отметим только очевидные свойства:
det(I ) = 1, det(A ) = det(A t),
det(AB ) = det(A )det(B ).
1.6. Векторы
Если матрица состоит только из одного столбца (J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например
Можно рассматривать и матрицы, состоящие из одной строки, например
![]()
Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело - со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.
Размерностью вектора называется число его элементов.
Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.

В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .
1.7. Простейшие операции с векторами
Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,

Рис. 13 Операции с векторами
Два вектора x и y называются колинеарными , если существует такое число α, что
1.8. Произведения векторов
Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = (x 1 , x 2 ,...,x N) t и y = (y 1 , y 2 ,..., y N) t . Руководствуясь правилом перемножения "строка на столбец", мы можем составить из них два произведения: x t y и xy t . Первое произведение
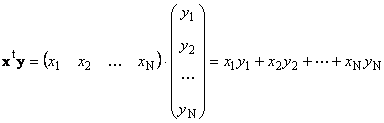
называется скалярным или внутренним . Его результат - это число. Для него также используется обозначение (x ,y )= x t y . Например,

Рис. 14 Внутреннее (скалярное) произведение
Второе произведение
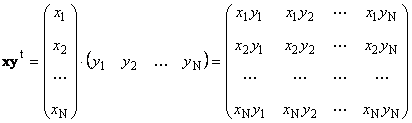
называется внешним . Его результат - это матрица размерности (N ×N ). Например,

Рис. 15 Внешнее произведение
Векторы, скалярное произведение которых равно нулю, называются ортогональными .
1.9. Норма вектора
Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина
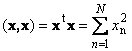
определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение
Например,

Рис. 16 Норма вектора
Вектор единичной длины (||x || = 1) называется нормированным. Ненулевой вектор (x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = ||x || (x/ ||x ||) = ||x || e . Здесь e = x/ ||x || - нормированный вектор.
Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.
1.10. Угол между векторами
Скалярное произведение определяет и угол φ между двумя векторами x и y
![]()
Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.
1.11. Векторное представление матрицы
Каждую матрицу A размера I ×J можно представить как набор векторов
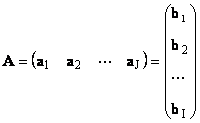
Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A
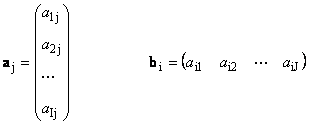
1.12. Линейно зависимые векторы
Векторы одинаковой размерности (N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 ,...,x K и столько же чисел α α 1 , α 2 ,...,α K . Вектор
y = α 1 x 1 + α 2 x 2 +...+ α K x K
называется линейной комбинацией векторов x k .
Если существуют такие ненулевые числа α k ≠ 0, k = 1,..., K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2x 2 = 0
1.13. Ранг матрицы
Рассмотрим набор из K векторов x 1 , x 2 ,...,x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе
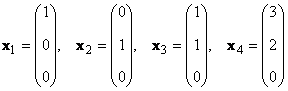
имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.
Очевидно, что если векторов в наборе больше, чем их размерность (K >N ), то они обязательно линейно зависимы.
Рангом матрицы (обозначается rank(A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.
1.14. Обратная матрица
Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями
AA −1 = A −1 A = I .
Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является
det(A ) ≠ 0 или rank(A ) = N .
Обращение матрицы - это сложная процедура, для выполнения которой существуют специальные программы. Например,

Рис. 17 Обращение матрицы
Приведем формулы для простейшего случая - матрицы 2×2
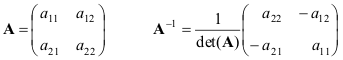
Если матрицы A и B невырождены, то
(AB ) −1 = B −1 A −1 .
1.15. Псевдообратная матрица
Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что
AA + A = A .
Псевдобратная матрица - не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза .
Если число столбцов меньше числа строк, то
A + =(A t A ) −1 A t
Например,

Рис. 17a Псевдообращение матрицы
Если же число столбцов больше числа строк, то
A + =A t (AA t) −1
1.16. Умножение вектора на матрицу
Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка - слева x t A . Если размерность вектора J , а размерность матрицы I ×J то в результате получится вектор размерности I . Например,

Рис. 18 Умножение вектора на матрицу
Если матрица A - квадратная (I ×I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что
A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .
Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .
2. Дополнительная информация
2.1. Системы линейных уравнений
Пусть A - матрица размером I ×J , а b - вектор размерности J . Рассмотрим уравнение
Ax = b
относительно вектора x , размерности I . По сути - это система из I линейных уравнений с J неизвестными x 1 ,...,x J . Решение существует в том, и только в том случае, когда
rank(A ) = rank(B ) = R ,
где B - это расширенная матрица размерности I ×(J+1 ), состоящая из матрицы A , дополненной столбцом b , B = (A b ). В противном случае уравнения несовместны.
Если R = I = J , то решение единственно
x = A −1 b .
Если R < I , то существует множество различных решений, которые можно выразить через линейную комбинацию J −R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A (N ×N ) имеет нетривиальное решение (x ≠ 0 ) тогда и только тогда, когда det(A ) = 0. Если R = rank(A )<N , то существуют N −R линейно независимых решений.
2.2. Билинейные и квадратичные формы
Если A - это квадратная матрица, а x и y - вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой, определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.
2.3. Положительно определенные матрицы
Квадратная матрица A называется положительно определенной , если для любого ненулевого вектора x ≠ 0 ,
x t Ax > 0.
Аналогично определяются отрицательно (x t Ax < 0), неотрицательно (x t Ax ≥ 0) и неположительно (x t Ax ≤ 0) определенные матрицы.
2.4. Разложение Холецкого
Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой
A = U t U .
Например,

Рис. 19 Разложение Холецкого
2.5. Полярное разложение
Пусть A - это невырожденная квадратная матрица размерности N ×N . Тогда существует однозначное полярное представление
A = SR,
где S - это неотрицательная симметричная матрица, а R - это ортогональная матрица. Матрицы S и R могут быть определены явно:
S 2 = AA t или S = (AA t) ½ и R = S −1 A = (AA t) −½ A .
Например,
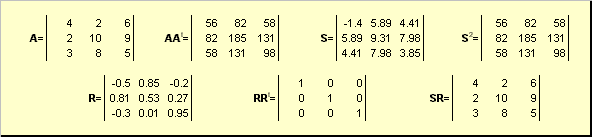
Рис. 20 Полярное разложение
Если матрица A вырождена, то разложение не единственно - а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .
2.6. Собственные векторы и собственные значения
Пусть A - это квадратная матрица. Вектор v называется собственным вектором матрицы A , если
Av = λv ,
где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v - собственный вектор, то и αv - тоже собственный вектор.
2.7. Собственные значения
У матрицы A , размерностью (N ×N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению
det(A − λI ) = 0,
являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид
Например,

Рис. 21 Собственные значения
Набор собственных значений λ 1 ,..., λ N матрицы A называется спектром A .
Спектр обладает разнообразными свойствами. В частности
det(A ) = λ 1 ×...×λ N , Sp(A ) = λ 1 +...+λ N .
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (A t = A ), то ее собственные значения вещественны.
2.8. Собственные векторы
У матрицы A , размерностью (N ×N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений
(A − λ n I ) v n = 0 .
Она имеет нетривиальное решение, поскольку det(A − λ n I ) = 0.
Например,

Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.