Нахождение определителя из системы уравнений. Большая энциклопедия нефти и газа. Три случая при решении систем линейных уравнений
Ответ:.Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
 ;
;
 .
.
Формулы Крамера для нахождения неизвестных:
![]() .
.
Найти значения и возможно только при условии, если
Этот вывод следует из следующей теоремы.
Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:


Итак, решение системы (2):
9.операции над множествами. диаграммы Вьена.
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
Операции над множествами рассматриваются для получения новых множеств из уже существующих.
Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):
 Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
11.отображения (функция), область определения, образы множеств при отображении, множество значений функции и её график.
Ответ: Отображением множества E в множество F, или функцией, определенной на E со значениями в F, называется правило, или закон f, который каждому элементу ставит в соответствие определенный элемент .
Элемент называют независимым элементом, или аргументом функции f, элемент называют значением функции f, илиобразом; при этом элемент называется прообразом элемента .
Отображение (функцию) обычно обозначают буквой f или символом , указывая тем самым, что f отображает множество E в F. Употребляется также обозначение , указывающее, что элементу x соответствует элемент f(x). Иногда функцию удобно задавать посредством равенства, в котором содержится закон соответствия. Например, можно говорить, что "функция f определена равенством ". Если "y" - общее наименование элементов множества F, т. е. F = {y}, то отображение записывают в виде равенстваy = f(x) и говорят, что это отображение задано явно.
2. Образ и прообраз множества при заданном отображении
Пусть задано отображение и множество .
Множество элементов из F, каждый из которых является образом хотя бы одного элемента из D при отображении f, называется образоммножества D и обозначается f(D).
Очевидно, .
Пусть теперь задано множество .
Множество элементов таких, что , называется прообразом множества Y при отображении f и обозначается f -1 (Y).
Если , то . Если при каждом множество f -1 (y) состоит не более чем из одного элемента , то f называетсявзаимно однозначным отображением E в F. Впрочем, можно определить взаимно однозначное отображение f множества E на F.
Отображение называется:
Инъективным (или инъекцией, или взаимно однозначным отображением множества E в F), если , или если уравнение f(x) = y имеет не более одного решения;
Сюръективным (или сюръекцией, или отображением множества E на F), если f(E) = F и если уравнение f(x) = y имеет по крайней мере одно решение;
Биективным (или биекцией, или взаимно однозначным отображением множества E на F), если оно инъективно и сюръективно, или если уравнение f(x) = y имеет одно и только одно решение.
3. Суперпозиция отображений. Обратное, параметрическое и неявное отображения
1) Пусть и . Поскольку , то отображение g каждому элементу относит определенный элемент .
Таким образом, каждому посредством правила поставлен в соответствие элемент
Тем самым определено новое отображение (или новая функция), которое назовем композицией отображений, или суперпозицией отображений, или сложным отображением.
2) Пусть - биективное отображение и F = {y}. В силу биективности f каждому соответствует единичный образ x, который обозначим через f -1 (y), и такой, что f(x) = y. Таким образом, определено отображение , которое называется обратным отображению f, или обратной функцией функции f.
Очевидно, отображение f обратно отображению f -1 . Поэтому отображения f и f -1 называют взаимно обратными. Для них справедливы соотношения
причем хотя бы одно из этих отображений, например , биективно. Тогда существует обратное отображение , а значит, .
Определенное таким образом отображение называется заданным параметрически с помощью отображений ; причем переменная из называется параметром.
4) Пусть на множестве определено отображение , где множество содержит нулевой элемент. Предположим, что существуют множества такие, что при каждом фиксированном уравнение имеет единственное решение . Тогда на множестве E можно определить отображение , ставящее каждому в соответствие то значение , которое при указанном x является решением уравнения .
Относительно так определенного отображения
говорят, что оно задано неявно посредством уравнения .
5) Отображение называется продолжением отображения , а g - сужением отображения f, если и .
Сужение отображения на множество иногда обозначают символом .
6) Графиком отображения называется множество
Ясно, что .
12. монотонные функции. Обратная функция, теорема существования. Функции y=arcsinx y=arcos x х свойства и графики.
Ответ: Моното́нная фу́нкция - это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю то функция называется стро́го моното́нной.
Пусть имеется функция f(x) определенная на отрезке
то говорят, что на отрезке
Обратите внимание на отличие этого определения от определения заполненности отрезка
Обычно, говоря об обратной функции, заменяют х на у а y на x(x «y) и пишут y=f (-1) (x). Очевидно, что исходная функция f(x) и обратная функция f (-1) (x) удовлетворяют соотношению
f (-1) (f(x))=f(f (-1) (x))=x.
Графики исходной и обратной функции получаются друг из друга зеркальным отображением относительно биссектрисы первого квадранта.
Теорема. Пусть функция f(x) определена, непрерывна и строго монотонно возрастает (убывает) на отрезке . Тогда на отрезке определена обратная функция f (-1) (x), которая также непрерывна и строго монотонно возрастает (убывает).
Доказательство.
Докажем теорему для случая, когда f(x) строго монотонно возрастает.
1. Существование обратной функции.
Так как по условию теоремы f(x) непрерывна, то, согласно предыдущей теореме, отрезок заполнен сплошь. Это означает, что.
Докажем, что х единственно. Действительно, если взять х’>x, то будет f(x’)>f(x)=y и поэтому f(x’)>y. Если взять х’’ 2. Монотонность обратной функции. Сделаем обычную замены x «y и будем писать y= f (-1) (x). Это значит, что x=f(y). Пусть x 1 >x 2 . Тогда: y 1 = f (-1) (x 1); x 1 =f(y 1) y 2 = f (-1) (x 2); x 2 =f(y 2) Какое же соотношение между y 1 и y 2 ? Проверим возможные варианты. а) y 1 б) y 1 =y 2 ? Но тогда f(y 1)=f(y 2) и x 1 =x 2 , а у нас было x 1 >x 2 . в) Остается единственный вариант y 1 >y 2 , т.е. Но тогда f (-1) (x 1)>f (-1) (x 2), а это и означает, что f (-1) (…) строго монотонно возрастает. 3. Непрерывность обратной функции. Т.к. значения обратной функции заполняют сплошь отрезок , то по предыдущей теоремеf (-1) (…) непрерывна. < <="" a="" style="color: rgb(255, 68, 0);"> <="" a="" style="color: rgb(0, 0, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);">
<="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);"> 13.композиция функций. Элементарные функции. Функции y=arctg x , y = arcctg x, их свойства и графики.
Ответ: В математике компози́ция фу́нкций (суперпози́ция фу́нкций) - это применение одной функции к результату другой. Композиция функций G и F обычно обозначается G∘F, что обозначает применение функции G к результату функции F. Пусть F:X→Y и G:F(X)⊂Y→Z две функции. Тогда их композицией называется функция G∘F:X→Z, определённая равенством: (G∘F)(x)=G(F(x)),x∈X. Элементарные функции - функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций : Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения. Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции. <="" a="" style="color: rgb(255, 68, 0); font-family: Arial; font-size: 11px; font-style: normal; font-variant: normal; font-weight: normal; letter-spacing: normal; line-height: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-stroke-width: 0px; background-color: rgb(0, 171, 160);"> Для краткости матрицу можно обозначать одной заглавной буквой, например, А
или В
.В общем виде матрицу размером m
×n
записывают так Числа, составляющие матрицу, называются элементами матрицы
. Элементы матрицы удобно снабжать двумя индексами a
ij
: первый указывает номер строки, а второй – номер столбца. Например, a
23
– элемент стоит во 2-ой строке, 3-м столбце.Если в матрице число строк равно числу столбцов, то матрица называется квадратной
, причём число ее строк или столбцов называется порядком
матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.Матрица, в которой число строк не равно числу столбцов, называется прямоугольной
. В примерах это первая матрица и третья.Различаются также матрицы, имеющие только одну строку или один столбец.Матрица, у которой всего одна строка , называется матрицей – строкой
(или строковой), а матрица, у которой всего один столбец, матрицей – столбцом
.Матрица, все элементы которой равны нулю, называется нулевой
и обозначается (0), или просто 0. Например, Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной
матрицей. Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной
матрицей. Например, или .Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной
матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид Таким образом, например, чтобы получить у произведения (т.е. в матрице C
) элемент, стоящий в 1-ой строке и 3-м столбце c
13
, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.В общем случае, если мы умножаем матрицу A = (a
ij
)
размера m
×n
на матрицу B = (b
ij
)
размера n
×p
, то получим матрицу C
размера m
×p
, элементы которой вычисляются следующим образом: элемент c
ij
получается в результате произведения элементов i
-ой строки матрицы A
на соответствующие элементы j
-го столбца матрицы B
и их сложения.Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно, Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.Определителем третьего порядка
, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом: Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a
11
, a
12
, a
13
и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.Примеры.
Вычислить определитель третьего порядка. Для определителя третьего порядка проверьте самостоятельно. Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:.Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем: Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c
22
= c
33
= 1. Кроме того, все недиагональные элементы матрицы C
равны нулю. Например, где A
ij
- алгебраические дополнения элементов a
ij
данной матрицы A
.Итак, чтобы найти обратную матрицу нужно: Аналогично для матриц второго порядка, обратной будет следующая матрица где a
ij
и b
i
(i
=1,…,m
; b
=1,…,n
) – некоторые известные числа, а x
1
,…,x
n
– неизвестные. В обозначении коэффициентов a
ij
первый индекс i
обозначает номер уравнения, а второй j
– номер неизвестного, при котором стоит этот коэффициент.Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы
.Числа, стоящие в правых частях уравнений, b
1
,…,b
m
называются свободными членами.
Совокупность n
чисел c
1
,…,c
n
называется решением
данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c
1
,…,c
n
вместо соответствующих неизвестных x
1
,…,x
n
.Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации: Система линейных уравнений, имеющая хотя бы одно решение, называется совместной
. В противном случае, т.е. если система не имеет решений, то она называется несовместной
.Рассмотрим способы нахождения решений системы.МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными: Рассмотрим матрицу системы т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных, называется определителем системы
.Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов Тогда можно доказать следующий результат.Теорема (правило Крамера).
Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём Сложим эти уравнения: Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца Аналогично можно показать, что и .Наконец несложно заметить, что Лекция 1.1.
Числовые матрицы и действия над ними.
Краткое содержание:
Место линейной алгебры и аналитической геометрии в естествознании. Роль отечественных ученых в развитии этих наук. Понятие матрицы. Операции над матрицами и их свойства.
Таблица чисел вида называется прямоугольной матрицей
размерности . Матрицы обозначаются заглавными латинскими буквами A, B, C,
…Числа, из которых состоит таблица, называют элементами
матрицы. Каждый элемент имеет два индекса и , обозначающие соответственно номер строки () и номер столбца(), в которых расположен данный элемент. Используются следующие обозначения матрицы . Две матрицы называются равными
, если они имеют одинаковую размерность (т.е. одинаковое число строк и столбцов) и если числа, стоящие на соответствующих местах этих матриц, равны. Если число строк матрицы равно числу ее столбцов, матрицу называют квадратной
. В квадратной матрице число строк (или столбцов) называют порядком матрицы. В частности квадратная матрица первого порядка – это просто действительное число. Соответственно говорят, что вектор строка
Элементы, стоящие на главной диагонали квадратной матрицы (идущей из левого верхнего в правый нижний угол), называются диагональными
. Квадратная матрица все элементы которой не лежащие на главной диагонали равны 0 называется диагональной
. Диагональная матрица, все диагональные элементы которой равны 1, а все внедиагональные – 0, называется единичной
и обозначается или , где n- ее порядок. Основные операции над матрицами – сложение матриц и умножение матрицы на число. Произведением
матрицы А
на число называется матрица той же размерности, что и матрица А,
каждый элемент которой умножен на это число . Например: Свойства операции умножения матрицы на число: 1. l(mА
)=(lm)А
(ассоциативность) 2. l(А
+В
)= lА
+lВ
(дистрибутивность относительно сложения матриц) 3. (l+m)А
=)=lА
+mА
(дистрибутивность относительно сложения чисел) Линейной комбинацией матриц А
и В
одинакового размера называется выражение вида: aА
+bВ
, где a,b - произвольные числа Суммой матрицА
и В
(это действие применимо только к матрицам одинаковой размерности) называется матрица С
такой же размерности, элементы которой равны суммам соответствующих элементов матриц А
и В
. Свойства сложения матриц: 1)А
+В
=В
+А
(коммутативность) 2)(А
+В
)+С
=А
+(В
+С
)=А
+В
+С
(ассоциативность) Разностью матрицА
и В
(это действие применимо только к матрицам одинаковой размерности) называется матрица С такой же размерности, элементы которой равны разности соответствующих элементов матриц А
и В
. Транспонирование
. Если элементы каждой строки матрица размерности записать в том же порядке в столбцы новой матрицы, причем номер столбца будет равен номеру строки, то новую матрицу называют транспонированной по отношению к и обозначают . Размерность равна Переход от к называется транспонированием. Ясно так же, что . Умножение матриц
. Операция умножения матриц возможна лишь в том случае, если число столбцов первого множителя равны числу строк второго. В результате умножения получим матрицу, число строк которой совпадает с числом строк первого множителя, а число столбцов с числом столбцов второго: Правило умножения матриц: чтобы получить элемент, стоящий в –й строке и –м столбце произведения двух матриц, нужно элементы –й строки первой матрицы умножить на элементы –го столбца второй матрицы и полученные произведения сложить. На математическом жаргоне иногда говорят: нужно –ую строку матрицы умножить на –й столбец матрицы . Ясно, что строка первой и столбец второй матрицы должны содержать одинаковое количество элементов. В отличие от этих операций операция умножения матрицы на матрицу определяется более сложно. Пусть заданы две матрицы А
и В
, причем число столбцов первой из них равно числу строк второй: например, матрица А
имеет размерность , а матрица В
– размерность . Если называется произведением матрицы А
на матрицу В
и обозначается АВ
. Свойства операции умножения матриц: 1. (АВ)С=А(ВС)=АВС
(ассоциативность) 2. (А+В)С=АС+ВС
(дистрибутивность) 3. А(В+С)=АВ+А
(дистрибутивность) 4. Умножение матриц некоммутативно: АВ
не равно ВА
., если равно, то эти матрицы называются перестановочными. Элементарные преобразования над матрицами
: 1. Перемена местами двух строк (столбцов) 2. Умножение строки (столбца) на число, отличное от нуля 3. Прибавление к элементам одной строки (столбца) элементов другой строки (столбца), умноженных на какое либо число Лекция 1.2.
Определители с действительными коэффициентами. Нахождение обратной матрицы.
Краткое содержание:
Определители и их свойства. Методы вычисления определителей с действительными коэффициентами. Нахождение обратной матрицы дляматриц третьего порядка.
Понятие определителя вводится только для квадратной матрицы. Определитель
– это число
, которое находится по вполне определенным правилам и обозначается или det A
. Определитель
матрицы второго порядка
находится так: или Определителем третьего порядка
называется число: Для запоминания этой громоздкой формулы существует «правило треугольников»: Можно посчитать и другим методом ‑ методом разложения по строке или по столбцу. Введем некоторые определения: Минором
квадратной матрицы А
называется определитель матрицы А
, который получается вычеркиванием –й строки и –го столбца: например для минор - Алгебраическим дополнением
элемента определителя называется его минор, взятый со своим знаком, если сумма номеров строки и столбца, в которых расположен элемент, четна, и с обратным знаком, если сумма номеров нечетна: . Тогда: Определитель третьего порядка
равен сумме произведений элементов какого-нибудь столбца (строки) на их алгебраические дополнения. ПР: Вычислим определитель: , разложив его по элементам первой строки. Свойства определителей: 1.Определитель равен 0, если содержит две одинаковые строки (столбца) или нулевую строку (столбец). 2.Определитель меняет свой знак при перестановке двух строк (столбцов). 3.Общий множитель в строке (в столбце) можно выносить за знак определителя. 4.Определитель не меняется, если к строке (столбцу) прибавить любую другую строку (другой столбец), умноженную на произвольное число. 5.Определитель не меняется при транспонировании матрицы . 6.Определитель еденичной матрицы равен 1: 7.Определитель произведения матриц равен произведению определителей Обратная матрица
. Квадратная матрица называется невырожденной
, если ее определитель отличен от нуля. Если при умножении квадратных матриц А
и В
в любом порядке получается единичная матрица (АВ=ВА=Е
), то матрица В
называется обратной матрицей для матрицы А
и обозначается , т.е. . Теорема.
Всякая невырожденная матрица имеет обратную
. Алгоритм нахождения обратной матрицы: Обратная матрица.
Квадратная матрица наз невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной.
Матрица, обратная к матрице обозначается . Если обратная матрица существует, то она единственна и Где – присоединенная (союзная), составленная из алгебраических дополнений j: Тогда определитель обратной матрицы связан с определителем данной матрицы следующим соотношением: . В самом деле, Свойства обратной матрицы: 1. 3. 4. Лекция 1.3.
Решение систем линейных уравнений методом Крамера.методам Гаусса и средствами матричного исчисления.
Краткое содержание:
Метод Крамера и метод Гаусса решения систем линейных алгебраических уравнений. Матричный способ решения систем уравнений. Ранг матрицы. Теорема Кронекера-Капелли. Фундаментальная система решений. Однородные и неоднородные системы.
Система уравнений следующего вида: Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения. Метод Крамера может быть использован в решении системы стольких линейных уравнений,
сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю,
то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Кроме того, метод Крамера может быть использован в решении систем линейных уравнений,
имеющих единственное решение. Определение
. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта). Определители получаются путём замены коэффициентов при соответствующих неизвестных свободными членами: Теорема Крамера
. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1.
Решить систему линейных уравнений: Согласно теореме Крамера
имеем: Итак, решение системы (2): онлайн-калькулятором , решающим методом Крамера. Как явствует из теоремы Крамера
, при решении системы линейных уравнений могут встретиться три случая: Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа) Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа) ** т.е. коэффициенты при неизвестных и свободные члены пропорциональны. Третий случай: система линейных уравнений решений не имеет
(система несовместна) Итак, система m
линейных уравнений с n
переменными называется несовместной
, если у неё нет ни одного решения, и совместной
, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой
, а более одного – неопределённой
. Пусть дана система На основании теоремы Крамера
…………. где определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами: Пример 2.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители По формулам Крамера находим: Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера. Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример. Пример 3.
Решить систему линейных уравнений методом Крамера: Решение. Находим определитель системы: Посмотрите внимательно на систему уравнений и на определитель системы и повторите
ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак,
определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных По формулам Крамера находим: Итак, решение системы - (2; -1; 1). Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера. Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных
не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером. Пример 6.
Решить систему линейных уравнений методом Крамера: Решение. Находим определитель системы: Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна
и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть
не имеет решений. Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера. В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко
ходить не надо. Следующий пример - на аналогичную задачу, только увеличивается количество уравнений,
переменных, и букв, обозначающих некоторое действительное число. Пример 8.
Решить систему линейных уравнений методом Крамера: Решение. Находим определитель системы: Находим определители при неизвестных Задана система N линейных алгебраических уравнений (СЛАУ) с неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами — числа Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй — при котором из неизвестным он находится. Если определитель матрицы не равен нулю то система линейных алгебраических уравнений имеет единственное решение. Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство. Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой. Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной. Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований. Эквивалентные преобразования СЛАУ 1) перестановка местами уравнений; 2) умножение (или деление) уравнений на отличное от нуля число; 3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число. Решение СЛАУ можно найти разными способами. МЕТОД КРАМЕРА ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера: Если , а хотя бы один из отличен от нуля, то СЛАУ решений не имеет. Если же ————————————————————— Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера Найдем определитель матрицы коэффициентов при неизвестных Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители: По формулам Крамера находим неизвестные Итак Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера. Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке. Найдем составляющие определителя: Подставим найденные значения в определитель Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера: Разложим каждый из определителей по столбцу в котором есть больше нулей. По формулам Крамера находим Решение системы Данный пример можно решить математическим калькулятором YukhymCALC
. Фрагмент программы и результаты вычислений наведены ниже. МЕТОД К Р А М Е Р А
|1,1,1,1|
D=|5,-3,2,-8|
|3,5,1,4|
|4,2,3,1|
D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10
|0,1,1,1|
Dx1=|1,-3,2,-8|
|0,5,1,4|
|3,2,3,1|
Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70
|1,0,1,1|
Dx2=|5,1,2,-8|
|3,0,1,4|
|4,3,3,1|
Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80
|1,1,0,1|
Dx3=|5,-3,1,-8|
|3,5,0,4|
|4,2,3,1|
Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50
|1,1,1,0|
Dx4=|5,-3,2,1|
|3,5,1,0|
|4,2,3,3|
Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60
x1=Dx1/D=70,0000/10,0000=7,0000
x2=Dx2/D=-80,0000/10,0000=-8,0000
x3=Dx3/D=-50,0000/10,0000=-5,0000
x4=Dx4/D=60,0000/10,0000=6,0000
Посмотреть материалы:
{jcomments on}
В общем случае правило вычисления определителей-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений. Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали: Пример
Задание.
Вычислить определитель второго порядка Решение.
Ответ.
Для вычисления определителей третьего порядка существует такие правила. Схематически это правило можно изобразить следующим образом: Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е. Пример
Задание.
Вычислить определитель Решение.
Ответ.
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»: Пример
Задание.
Вычислить определитель Решение.
Ответ.
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой. Пример
Задание.
Разложив по первой строке, вычислить определитель Решение.
Ответ.
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка. Пример
Задание.
Вычислить определитель Решение.
Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному. Определитель равен нулю, так как вторая и третья строки являются пропорциональными. Ответ.
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа. Пример
Задание.
Вычислить определитель Решение.
Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем: Полученный определитель разложим по элементам первого столбца: Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую: Ответ.
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки. С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали. Пример
Задание.
Вычислить определитель Решение.
Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный: Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя): Ответ.
Пример
Задание.
Используя теорему Лапласа, вычислить определитель Решение.
Выберем в данном определителе пятого порядка две строки — вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем): Ответ.
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА I
§ 31 Случай, когда главный определитель системы уравнений равен нулю, а хотя бы один из вспомогательных определителей отличен от нуля
Теорема.
Если главный определитель системы уравнений
равен нулю, а хотя бы один из вспомогательных определителей отличен от нуля, то система несовместна.
Формально, доказательство этой теоремы нетрудно получить методом от противного. Предположим, что система уравнений (1) имеет решение (x
0 , y
0). Тогда как показано в предыдущем параграфе, Δ
x
0 = Δ x
, Δ
y
0 = Δ y
(2) Но по условию Δ
= 0, а хотя бы один из определителей Δ x
и Δ y
отличен от нуля. Таким образом, равенства (2) одновременно выполняться не могут. Теорема доказана. Однако представляется интересным более детально выяснить, почему система уравнений (1) в рассматриваемом случае несовместна. означает, что коэффициенты при неизвестных в системе уравнений (1) пропорциональны. Пусть, например, a
1 = ka
2 , b
1 = kb
2 .
означает, что коэффициенты при у
и свободные члены уравнений системы (1) не пропорциональны. Поскольку b
1 = kb
2 , то c
1 =/= kc
2 . Следовательно, система уравнений (1) может быть записана в следующем виде: В этой системе коэффициенты при неизвестных соответственно пропорциональны, но коэффициенты при у
(или при х
) и свободные члены не пропорциональны. Такая система, конечно, несовместна. Действительно, если бы она имела решение (x
0 , y
0), то выполнялись бы числовые равенства k
(a
2 x
0 + b
2 y
0) = c
1 a
2 x
0 + b
2 y
0 = c
2 . Но одно из этих равенств противоречит другому: ведь c
1 =/= kc
2 . Мы рассмотрели лишь случай, когда Δ x
=/= 0. Аналогично может быть рассмотрен случай, когда Δ y
=/= 0." Доказанную теорему можно сформулировать и таким образом. Если коэффициенты при неизвестных х
и у
в системе уравнений (1) пропорциональны, а коэффициенты при какой-нибудь из этих неизвестных и свободные члены не пропорциональны, то эта система уравнений несовместна.
Легко, например, убедиться в том, что каждая из данных систем будет несовместной: Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения. Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение. Определение
. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта). Определители получаются путём замены коэффициентов при соответствующих неизвестных свободными членами: Теорема Крамера
. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1.
Решить систему линейных уравнений: Согласно теореме Крамера
имеем: Итак, решение системы (2): Как явствует из теоремы Крамера
, при решении системы линейных уравнений могут встретиться три случая: Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа) * Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа) ** т.е. коэффициенты при неизвестных и свободные члены пропорциональны. Третий случай: система линейных уравнений решений не имеет
(система несовместна) Итак, система m
линейных уравнений с n
переменными называется несовместной
, если у неё нет ни одного решения, и совместной
, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой
, а более одного – неопределённой
. Пусть дана система На основании теоремы Крамера …………. где определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами: Пример 2.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители По формулам Крамера находим: Итак, (1; 0; -1) – единственное решение системы. Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера. Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример. Пример 3.
Решить систему линейных уравнений методом Крамера: Решение. Находим определитель системы: Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных По формулам Крамера находим: Итак, решение системы — (2; -1; 1). Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера. Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером. Пример 4.
Решить систему линейных уравнений методом Крамера: Решение. Находим определитель системы: Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений. Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера. В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо. Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число. Пример 6.
Решить систему линейных уравнений методом Крамера: Решение. Находим определитель системы: Находим определители при неизвестных По формулам Крамера находим: И, наконец, система четырёх уравнений с четырьмя неизвестными. Пример 7.
Решить систему линейных уравнений методом Крамера: Внимание! Методы вычисления определителей четвёртого порядка здесь объясняться не будут. За этим — на соответствующий раздел сайта. Но небольшие комментарии будут. Решение. Находим определитель системы: Небольшой комментарий. В первоначальном определителе из элементов второй строки были вычтены элементы четвёртой строки, из элементов третьей строки — элементы четвёртой строки, умноженной на 2, из элементов четвёртой строки — элементы первой строки, умноженной на 2. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Находим определители при неизвестных Для преобразований определителя при четвёртом неизвестном из элементов первой строки были вычтены элементы четвёртой строки. По формулам Крамера находим: Итак, решение системы — (1; 1; -1; -1). Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера. Самые внимательные, наверное, заметили, что в статье не было примеров решения неопределённых систем линейных уравнений. А всё потому, что методом Крамера решить такие системы невозможно, можно лишь констатировать, что система неопределённа. Решения таких систем даёт метод Гаусса. Нет времени вникать в решение? Можно заказать работу! К началу страницы Пройти тест по теме Системы линейных уравнений Другое по теме «Системы уравнений и неравенств» Калькулятор — решение систем уравнений онлайн Программная реализация метода Крамера на C++ Решение систем линейных уравнений методом подстановки и методом сложения Решение систем линейных уравнений методом Гаусса Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли Решение систем линейных уравнений матричным методом (обратной матрицы) Системы линейных неравенств и выпуклые множества точек Начало темы «Линейная алгебра» Определители В этой статье мы познакомимся с очень важным понятием из раздела линейной алгебры, которое называется определитель. Сразу хотелось бы отметить важный момент: понятие определитель действительно только для квадратных матриц (число строк = числу столбцов), у других матриц его нет. Определитель квадратной матрицы
(детерминант) — численная характеристика матрицы. Обозначение определителей: |A|, det A, ∆
A. Определителем
«n» порядка называют алгебраическую сумму всех возможных произведений его элементов, удовлетворяющих следующим требованиям: 1) Каждое такое произведение содержит ровно «n» элементов (т.е. определитель 2 порядка — 2 элемента). 2) В каждом произведении присутствует в качестве сомножителя представитель каждой строки и каждого столбца. 3) Любые два сомножителя в каждом произведении не могут принадлежать одной строке или столбцу. Знак произведения определяется порядком чередования номеров столбцов, если в произведении элементы расставлены в порядке возрастания номеров строк. Рассмотрим несколько примеров нахождения детерминанта матрицы: У матрицы первого порядка (т.е. имеется всего 1 элемент), детерминант равен этому элементу: 2. Рассмотрим квадратную матрицу второго порядка: 3. Рассмотрим квадратную матрицу третьего порядка (3×3): 4. А теперь рассмотрим примеры с действительными числами: Правило треугольника. Правило треугольника — это способ вычисления определителя матрицы, который предполагает его нахождение по следующей схеме: Как вы уже поняли, метод был назван правилом треугольника в следствии того, что перемножаемые элементы матрицы образуют своеобразные треугольники. Для того, чтобы понять это лучше, разберём такой пример: А теперь рассмотрим вычисление определителя матрицы с действительными числами правилом треугольника: Для закрепления пройденного материала, решим ещё один практический пример: Свойства определителей: 1. Если элементы строки или столбца равны нулю, то и определитель равен нулю. 2. Определитель изменит знак, если поменять местами какие-либо 2 строки или столбца. Рассмотрим это на небольшом примере: 3. Определитель транспонированной матрицы равен определителю исходной матрицы. 4. Определитель равен нулю, если элементы одной строки равны соответствующим элементам другой строки (для столбцов также). Самый простой пример этого свойства определителей: 5. Определитель равен нулю, если его 2 строки пропорциональны (также и для столбцов). Пример (1 и 2 строка пропорциональны): 6. Общий сомножитель строки (столбца) может быть вынесен за знак определителя. 7) Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одну и ту же величину. Рассмотрим это на примере: Просмотры: 57258 Определитель(он же determinant(детерминант)) находится только у квадратных матриц. Определитель есть ничто иное, как значение сочетающее в себе все элементы матрицы, сохранающееся при транспонировании строк или столбцов. Обозначаться он может как det(A), |А|, Δ(A), Δ, где А может быть как матрицей, так и буквой обозначающей ее. Найти его можно разными методами: Все выше предложенные методы будут разобраны на матрицах размера от трех и выше. Определитель двумерной матрицы находится с помощью трех элементарных математических операций, поэтому ни в один из методов нахождение определителя двумерной матрицы не попадет. Ну кроме как дополнение, но об этом потом. Найдем определитель матрицы размером 2х2: Для того, чтобы найти определитель нашей матрицы, требуется вычесть произведение чисел одной диагонали из другой, а именно , то есть Примеры нахождения определителя матриц второго порядка Разложение по строке/столбцу
Выбирается любая строка или столбец в матрице. Каждое число в выбранной линии умножается на (-1) i+j где(i,j — номер строки,столбца того числа) и перемножается с определителем второго порядка, составленного из оставшихся элементов после вычеркивания i — строки и j — столбца. Разберем на матрице Например возьмем вторую строку. Примечание:
Если явно не указано, с помощью какой линии найти определитель, выбирайте ту линию у которой есть ноль. Меньше будет вычислений. Не трудно определить, что знак у числа меняется через раз. Поэтому вместо единиц можно руководствоваться такой таблицей: Решение можно написать так: Примеры нахождения определителя разложением по строке/столбцу: Метод приведения к треугольному виду(с помощью элементарных преобразований)
Определитель находится с помощью приведения матрицы к треугольному(ступенчатому) виду и перемножению элементов на главной диагонали Треугольной матрицей называется матрица, элементы которой по одну сторону диагонали равны нулю. При построении матрицы следует помнить три простых правила: Попытаемся получить нули в первом столбце, потом во втором. Взглянем на нашу матрицу: Та-а-ак. Чтобы вычисления были поприятнее, хотелось бы иметь самое близкое число сверху. Можно и оставить, но не надо. Окей, у нас во второй строке двойка, а на первой четыре. Поменяем же эти две строки местами. Поменяли строки местами, теперь мы должны либо поменять у одной строки знак, либо в конце поменять знак у определителя. Сделаем это потом. Теперь, чтобы получить ноль в первой строке — умножим первую строку на 2. Отнимем 1-ю строку из второй. Согласно нашему 3-му правилу возващаем исходную строку в начальное положение. Теперь сделаем ноль в 3-ей строке. Можем домножить 1-ую строку на 1.5 и отнять от третьей, но работа с дробями приносит мало удовольствия. Поэтому найдем число, к которому можно привести обе строки — это 6. Умножим 3-ю строку на 2. Теперь умножим 1-ю строку на 3 и отнимем из 3-ей. Возвратим нашу 1-ю строку. Не забываем, что умножали 3-ю строку на 2, так что потом разделим определитель на 2. Один столбец есть. Теперь для того чтобы получить нули во втором — забудем про 1-ю строку — работаем со 2-й строкой. Домножим вторую строку на -3и прибавим к третьей. Не забываем вернуть вторую строку. Вот мы и построили треугольнаую матрицу. Что нам осталось? А осталось перемножить числа на главной диагонали, чем и займемся. Ну и осталось вспомнить, что мы должны разделить наш определитель на 2 и поменять знак. Правило Саррюса(Правило треугольников)
Правило Саррюса применимо только к квадратным матрицам третьего порядка. Определитель вычисляется путем добавления первых двух столбцов справа от матрицы, перемножением элементов диагоналей матрицы и их сложением, и вычитанием суммы противоположных диагоналей. Из оранжевых диагоналей вычитаем фиолетовые. У правила треугольников то же, только картинка другая. Теорема Лапласа см. Разложение по строке/столбцу
y = arcsin x
y = arccos x
функция обратная функции y = sin x, - / 2 x / 2
функция обратная функции y = cos x, 0 x


y = arctg x
y = arcctg x
функция обратная функции y = tg x, - / 2 < x < / 2
функция обратная функции y = ctg x, 0 < x <
y > 0 при x R
ЭКСТРЕМУМЫ:
нет
нет
ПРОМЕЖУТКИ МОНОТОННОСТИ:
возрастает при x R
убывает при x R
МАТРИЦЫ, ОПРЕДЕЛИТЕЛИ, СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m
×n
называется совокупность m·n
чисел, расположенных в виде прямоугольной таблицы из m
строк и n
столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:  .
. .
. .
. .ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц
. Две матрицы A
и B
называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a
ij
= b
ij
. Так если
.ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц
. Две матрицы A
и B
называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a
ij
= b
ij
. Так если  и
и  , то A=B
, если a
11
= b
11
, a
12
= b
12
, a
21
= b
21
и a
22
= b
22
.Транспонирование
. Рассмотрим произвольную матрицу A
из m
строк и n
столбцов. Ей можно сопоставить такую матрицу B
из n
строк и m
столбцов, у которой каждая строка является столбцом матрицы A
с тем же номером (следовательно, каждый столбец является строкой матрицы A
с тем же номером). Итак, если
, то A=B
, если a
11
= b
11
, a
12
= b
12
, a
21
= b
21
и a
22
= b
22
.Транспонирование
. Рассмотрим произвольную матрицу A
из m
строк и n
столбцов. Ей можно сопоставить такую матрицу B
из n
строк и m
столбцов, у которой каждая строка является столбцом матрицы A
с тем же номером (следовательно, каждый столбец является строкой матрицы A
с тем же номером). Итак, если  , то
, то  .Эту матрицу B
называют транспонированной
матрицей A
, а переход от A
к B транспонированием
.Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A
, обычно обозначают A
T
.Связь между матрицей A
и её транспонированной можно записать в виде .Например.
Найти матрицу транспонированную данной.
.Эту матрицу B
называют транспонированной
матрицей A
, а переход от A
к B транспонированием
.Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A
, обычно обозначают A
T
.Связь между матрицей A
и её транспонированной можно записать в виде .Например.
Найти матрицу транспонированную данной.  Сложение матриц.
Пусть матрицы A
и B
состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры
. Тогда для того, чтобы сложить матрицы A
и B
нужно к элементам матрицы A
прибавить элементы матрицы B
, стоящие на тех же местах. Таким образом, суммой двух матриц A
и B
называется матрица C
, которая определяется по правилу, например,
Сложение матриц.
Пусть матрицы A
и B
состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры
. Тогда для того, чтобы сложить матрицы A
и B
нужно к элементам матрицы A
прибавить элементы матрицы B
, стоящие на тех же местах. Таким образом, суммой двух матриц A
и B
называется матрица C
, которая определяется по правилу, например, ![]()
 Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A
и ассоциативному (A+B
)+C
=A
+(B+C
).Умножение матрицы на число.
Для того чтобы умножить матрицу A
на число k
нужно каждый элемент матрицы A
умножить на это число. Таким образом, произведение матрицы A
на число k
есть новая матрица, которая определяется по правилу
Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A
и ассоциативному (A+B
)+C
=A
+(B+C
).Умножение матрицы на число.
Для того чтобы умножить матрицу A
на число k
нужно каждый элемент матрицы A
умножить на это число. Таким образом, произведение матрицы A
на число k
есть новая матрица, которая определяется по правилу  или .Для любых чисел a
и b
и матриц A
и B
выполняются равенства:
или .Для любых чисел a
и b
и матриц A
и B
выполняются равенства: ![]() Примеры.
Примеры.
 .
.  Матрицу C
найти нельзя, т.к. матрицы A
и B
имеют разные размеры.Умножение матриц.
Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением
матрицы A
не матрицу B
называется новая матрица C=AB
, элементы которой составляются следующим образом:
Матрицу C
найти нельзя, т.к. матрицы A
и B
имеют разные размеры.Умножение матриц.
Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением
матрицы A
не матрицу B
называется новая матрица C=AB
, элементы которой составляются следующим образом:  .
. Найти элементы c
12
, c
23
и c
21
матрицы C
.
Найти элементы c
12
, c
23
и c
21
матрицы C
. Найти произведение матриц.
 .
.  Найти АВ
и ВА
.
Найти АВ
и ВА
. 
 Найти АВ
и ВА
. , B·A
– не имеет смысла.Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B
≠
B∙A
. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC)
и (A+B)C=AC+BC
.Легко также проверить, что при умножении квадратной матрицы A
на единичную матрицу E
того же порядка вновь получим матрицу A
, причём AE=EA=A
.Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.Например
, если
Найти АВ
и ВА
. , B·A
– не имеет смысла.Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B
≠
B∙A
. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC)
и (A+B)C=AC+BC
.Легко также проверить, что при умножении квадратной матрицы A
на единичную матрицу E
того же порядка вновь получим матрицу A
, причём AE=EA=A
.Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.Например
, если  , то
, то ![]() .
. .Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.Примеры.
Вычислить определители второго порядка.
.Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.Примеры.
Вычислить определители второго порядка. ![]()

 .
. . (x
+3)(4x
-4-3x
)+4(3x
-4x
+4)=0. (x
+3)(x
-4)+4(-x
+4)=0. (x
-4)(x
-1)=0. x
1
= 4, x
2
= 1.Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки "+" и "–" у слагаемых чередуются.Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
. (x
+3)(4x
-4-3x
)+4(3x
-4x
+4)=0. (x
+3)(x
-4)+4(-x
+4)=0. (x
-4)(x
-1)=0. x
1
= 4, x
2
= 1.Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки "+" и "–" у слагаемых чередуются.Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
 Доказательство
проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа:
Доказательство
проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа: 
При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную величину, т.е., например,
Доказательство
проводится аналогично доказательству свойства 1 сравнением обеих частей. Проведём его для определителя второго порядка.  Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A
| = –|A
| или |A
| = 0.
Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A
| = –|A
| или |A
| = 0.  Доказательство
проводится проверкой, как и свойство 1. (Самостоятельно)
Доказательство
проводится проверкой, как и свойство 1. (Самостоятельно) Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю. (Доказательство – проверкой). Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,
 .
. Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины. Например,
 . Докажем это равенство, используя предыдущие свойства определителя.
. Докажем это равенство, используя предыдущие свойства определителя.  Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ
Пусть имеем определитель третьего порядка:
Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ
Пусть имеем определитель третьего порядка:  .Минором
, соответствующим данному элементу a
ij
определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i
-ой строки и j
-го столбца. Миноры соответствующие данному элементу a
ij
будем обозначать M
ij
.Например
, минором M
12
, соответствующим элементу a
12
, будет определитель
.Минором
, соответствующим данному элементу a
ij
определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i
-ой строки и j
-го столбца. Миноры соответствующие данному элементу a
ij
будем обозначать M
ij
.Например
, минором M
12
, соответствующим элементу a
12
, будет определитель  , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a
12
, берётся со знаком “–”, т.е. можно записать, что
, который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a
12
, берётся со знаком “–”, т.е. можно записать, что
Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.Введём ещё одно понятие.Алгебраическим дополнением
элемента a
ij
определителя называется его минор M
ij
, умноженный на (–1) i+j .Алгебраическое дополнение элемента a
ij
обозначается A
ij
.Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A
ij
= (–1) i+j M
ij
.
Например, Пример.
Дан определитель . Найти A
13
, A
21
, A
32
.
 Разложим полученный определитель по элементам 1-ой строки.
Разложим полученный определитель по элементам 1-ой строки.
Отсюда  .
.
 т.к. определители второго порядка в формуле (2) есть миноры элементов a
21
, a
22
, a
23
. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.Таким образом, справедлива следующая теорема.Теорема (о разложении определителя по заданной строке или столбцу).
Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.Всё вышесказанное справедливо и для определителей любого более высокого порядка.Примеры.
т.к. определители второго порядка в формуле (2) есть миноры элементов a
21
, a
22
, a
23
. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.Таким образом, справедлива следующая теорема.Теорема (о разложении определителя по заданной строке или столбцу).
Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.Всё вышесказанное справедливо и для определителей любого более высокого порядка.Примеры.

Вычислить определитель, используя его свойства. Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к определителям третьего порядка, преобразуем его, используя свойство 7, сделав в какой–либо строке или столбце все элементы, кроме одного, равными нулю. В данном случае удобно рассмотреть 4-й столбец или 4-ю строку:

ОБРАТНАЯ МАТРИЦА
Понятие обратной матрицы вводится только для квадратных матриц
.Если A
– квадратная матрица, то обратной
для неё матрицей называется матрица, обозначаемая A
-1
и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел)Справедлива следующая теорема:Теорема.
Для того чтобы квадратная матрица A
имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.Доказательство
: Необходимость
. Пусть для матрицы A
существует обратная матрица A
-1
. Покажем, что |A
| ≠ 0.
Прежде всего заметим, что можно доказать следующее свойство определителей . Предположим, что |A
| = 0. Тогда ![]() . Но с другой стороны
. Но с другой стороны ![]() . Полученное противоречие и доказывает, что |A
| ≠ 0.
. Полученное противоречие и доказывает, что |A
| ≠ 0.  Покажем, что в этом случае обратной матрицей будет матрица
Покажем, что в этом случае обратной матрицей будет матрица  , где A
ij
алгебраическое дополнение элемента a
ij
. Найдём AB=C
. Заметим, что все диагональные элементы матрицы C
будут равны 1. Действительно, например,
, где A
ij
алгебраическое дополнение элемента a
ij
. Найдём AB=C
. Заметим, что все диагональные элементы матрицы C
будут равны 1. Действительно, например,  Следовательно, AB=E
. Аналогично можно показать, что BA=E
. Поэтому B = A
-1
.Таким образом, теорема содержит способ нахождения обратной матрицы.Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом
Следовательно, AB=E
. Аналогично можно показать, что BA=E
. Поэтому B = A
-1
.Таким образом, теорема содержит способ нахождения обратной матрицы.Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом  ,
, .Примеры.
|A
| = 2. Найдем алгебраические дополнения элементов матрицы A
.
.Примеры.
|A
| = 2. Найдем алгебраические дополнения элементов матрицы A
.  Проверка:
Проверка:  . Аналогично A∙A
-1
= E
.
. Аналогично A∙A
-1
= E
.  . Вычислим |A
| = 4. Тогда
. Вычислим |A
| = 4. Тогда ![]() .
. ![]() .
. 

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Системой m линейных уравнений с n неизвестными
называется система вида 

 и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов  Найдем произведение
Найдем произведение 
 или короче A
∙X=B
.Здесь матрицы A
и B
известны, а матрица X
неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением
.Пусть определитель матрицы отличен от нуля |A
| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A
-1
, обратную матрице A
: . Поскольку A
-1
A = E
и E
∙X = X
, то получаем решение матричного уравнения в виде X = A
-1
B
.Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных
. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A
не будет квадратной и поэтому нельзя найти решение системы в виде X = A
-1
B
.Примеры.
Решить системы уравнений.
или короче A
∙X=B
.Здесь матрицы A
и B
известны, а матрица X
неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением
.Пусть определитель матрицы отличен от нуля |A
| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A
-1
, обратную матрице A
: . Поскольку A
-1
A = E
и E
∙X = X
, то получаем решение матричного уравнения в виде X = A
-1
B
.Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных
. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A
не будет квадратной и поэтому нельзя найти решение системы в виде X = A
-1
B
.Примеры.
Решить системы уравнений.  Найдем матрицу обратную матрице A
. ,
Найдем матрицу обратную матрице A
. ,  Таким образом, x
= 3, y
= – 1.
Таким образом, x
= 3, y
= – 1.  Итак, х
1 =4,х
2 =3,х
3 =5.
Итак, х
1 =4,х
2 =3,х
3 =5. ![]() Выразим искомую матрицу X
из заданного уравнения.
Выразим искомую матрицу X
из заданного уравнения.  Найдем матрицу А
-1 .
Найдем матрицу А
-1 .  Проверка:
Проверка:  Из уравнения получаем
Из уравнения получаем ![]() .
.  Следовательно,
Следовательно,![]() ПРАВИЛО КРАМЕРА
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
ПРАВИЛО КРАМЕРА
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными: 
![]()

 Таким образом, получаем равенство: .Следовательно, .Аналогично выводятся равенства и , откуда и следует утверждение теоремы.Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.Примеры.
Решить систему уравнений
Таким образом, получаем равенство: .Следовательно, .Аналогично выводятся равенства и , откуда и следует утверждение теоремы.Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.Примеры.
Решить систему уравнений  Итак, х
=1, у
=2, z
=3.
Итак, х
=1, у
=2, z
=3. ![]() Система имеет единственное решение, если Δ ≠ 0.
Система имеет единственное решение, если Δ ≠ 0. ![]() . Поэтому . МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
. Поэтому . МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:  .
.![]() есть матрица размерности , а вектор-столбец
имеет размерность .
есть матрица размерности , а вектор-столбец
имеет размерность .
![]() ;
; ![]() .
.



 ,
, 
![]()
 ,
,  , то матрица размерности
, то матрица размерности  , где (i=1,…,m;j=1,…,k)
, где (i=1,…,m;j=1,…,k) .
.![]() .
.![]()
![]()

![]() , откуда и следует данное равенство.
, откуда и следует данное равенство.![]() , где ‑ невырожденные квадратные матрицы одинакового порядка.
, где ‑ невырожденные квадратные матрицы одинакового порядка.![]() .
.![]()
 (*) , где , ‑ коэффициенты, ‑ переменные, называется системой линейных уравнений.
Решить систему линейных уравнений – это значит указать все решения системы, т.е. такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется.
(*) , где , ‑ коэффициенты, ‑ переменные, называется системой линейных уравнений.
Решить систему линейных уравнений – это значит указать все решения системы, т.е. такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется. ;
; .
.

Три случая при решении систем линейных уравнений


![]() ,
,
Примеры решения систем линейных уравнений методом Крамера
 .
.
, -
-


 .
.



![]()
Итак, (1; 0; -1) – единственное решение системы. .
.



К началу страницы
Продолжаем решать системы методом Крамера вместе




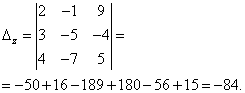

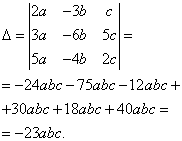



![]()
![]()
![]() — определители, образованные с заменой -го столбца, столбцом из свободных членов.
— определители, образованные с заменой -го столбца, столбцом из свободных членов.![]() , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.
, то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.




![]() единственное решение системы.
единственное решение системы.









![]()

——————————Вычисления определителей второго порядка
![]()
![]()
Методы вычисления определителей третьего порядка
Правило треугольника

 методом треугольников.
методом треугольников.

Правило Саррюса

 с помощью правила Саррюса.
с помощью правила Саррюса.

Разложение определителя по строке или столбцу




Разложение определителя по элементам строки или столбца
 , разложив его по элементам какой-то строки или какого-то столбца.
, разложив его по элементам какой-то строки или какого-то столбца.



Замечание
Приведение определителя к треугольному виду
 приведением его к треугольному виду.
приведением его к треугольному виду.4.Свойства определителей. Определитель произведения матриц.






Теорема Лапласа



![]() (1)
(1)





Метод Крамера решения систем линейных уравнений
Формулы Крамера
Метод Крамера. Применение для систем линейных уравнений
 ;
; .
.

Три случая при решении систем линейных уравнений



 ,
,
Примеры решения систем линейных уравнений методом Крамера
 .
.
, —
—


 .
.


![]()
 .
.



К началу страницы
Пройти тест по теме Системы линейных уравнений










![]() ,
,![]() ,
,![]() .
. .
.





![]()
![]()
![]()
Линейные уравнения. Решение систем линейных уравнений. Метод Крамера.













Определители. Вычисление определителей (стр. 2)





