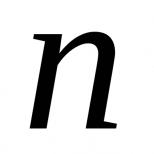Предельный переход. Предельный переход и непрерывность

Определение 1. Функция f(x) называется непрерывной в точке х = а, если она определена в некоторой двусторонней окрестности этой точки, включая и саму эту точку, и при этом

Функция называется непрерывной на промежутке, если она непрерывна во всех точках этого промежутка.

Точки разрыва и их типы

Определение 2. Точка х = а называется точкой устранимого разрыва, если в этой точке функция имеет равные между собой конечные пределы, но сама в этой точке либо принимает другое значение, либо вообще не определена.

Определение 3. Точка х = а называется точкой разрыва первого рода, если в этой точке функция имеет конечные, но различные односторонние пределы. При этом разность

f(a + 0) - f(a - 0)

называется скачком функции в точке х = а.

Определение 4. Точка х = а называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или равен .

Теорема 1. Если функции f(x) и g(x) непрерывны в точке х = а, то функции f(x) ± g(x), f(x) g(x), , где g(a) 0 также непрерывны в этой точке.

Теорема 2. Если функция f(x) непрерывна в точке х = а, а функция g(y) непрерывна в точке у = b, b = f(a), то сложная функция g(f(x)) непрерывна в точке х = а.

Теорема 3. Все элементарные функции непрерывны во всех точках, где они определены.

©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-07-22

Некоторая функция f будет стремится к числу А при х стремящемся к точке х0 тогда, когда разность f(x) – A будет сколь угодно мала. Другими словами, выражение |f(x) –A| становится меньше любого наперед заданного фиксированного числа h > 0, при уменьшении модуля приращения аргумента |∆x|.

Предельный переход

Нахождение этого числа А по функции f называют предельным переходом . В школьном курсе предельный переход будет встречаться в двух основных случаях.

1. Предельный переход в отношении ∆f/∆x при нахождении производной.

2. При определении непрерывности функции.

Непрерывность функции

Функция называется непрерывной в точке х0, если f(x) стремится к f(x0) при стремлении x к x0. При этом: f(x) – A = f(x) – f(x0) = ∆f.
Это означает, что |∆f| будет малым при малых |∆x|. Если описывать словами, то малым изменениям аргумента соответствуют малые изменения значения функции.

Функции, которые встречаются в школьном курсе математики, например, линейная функция, квадратичная функция, степенная функция и другие, непрерывны в каждой точке области, на которой они определены. У этих функций графики изображаются непрерывными кривыми линиями.

На этом факте основывается способ построения графика функции «по точкам», которым мы обычно пользуемся. Но прежде чем им пользоваться, необходимо выяснить действительно ли рассматриваемая функция будет непрерывна. Для простых случаев это можно сделать на основании определения непрерывности, которое мы дали выше.

Например: докажем, что линейная функция непрерывна в каждой точке числовой прямой y = k*x + b .

Согласно определению, нам нужно показать, что |∆f| становится меньше любого наперед заданного числа h>0, при малых |∆x|

|∆f| = |f(x0 +∆x) – f(x0)| = |(k*(x0+ ∆x) +b) – (k*x0+ b)| =|k|*|∆x|.

Если взять |∆x| >h/|k| при k не равном нулю, то |∆f| будет меньше любого h>0, что и требовалось доказать.

Правила предельного перехода

При использовании операции предельного перехода следует руководствоваться следующими правилами.

1. Если функция f непрерывна в точке x0, то ∆f стремится к нулю при стремлении ∆х к нулю.

2. Если функция f имеет производную в точке х0, то ∆f/∆x стремится к f’(x0) при стремлении ∆x к нулю.

3. Пусть f(x) стремится к A, g(x) стремится к B при стремлении х к х0. Тогда:

f(x) + g(x) стремится к A + B;

Свойства сходящихся последовательностей (ограниченность, арифметические свойства)

Ответ:

Если каждому натуральному числу n поставлено в соответствие число х n , то говорят, что задана последовательность

x 1, х 2 , …, х n = {x n }

Общий элемент последовательности является функцией от n.

Таким образом последовательность может рассматриваться как функция порядкового номера элемента.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример. {x n } = {(-1) n } или {x n } = -1; 1; -1; 1; …

{x n } = {sinpn/2} или {x n } = 1; 0; 1; 0; …

Для последовательностей можно определить следующиеарифметические свойства :

1) Умножение последовательности на число m: m{x n } = {mx n }, т.е. mx 1 , mx 2 , …

2) Сложение (вычитание) последовательностей: {x n } ± {y n } = {x n ± y n }.

3) Произведение последовательностей: {x n }×{y n } = {x n ×y n }.

4) Частное последовательностей: при {y n } ¹ 0.

Ограниченные и неограниченные последовательности.

Определение. Последовательность {x n } называется ограниченной , если существует такое число М>0, что для любого n верно неравенство:

т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение. ограниченной сверху

Определение. Последовательность {x n }называется ограниченной снизу , если для любого n существует такое число М, что

Пример. {x n } = n – ограничена снизу {1, 2, 3, … }.

Предельный переход в неравенствах для последовательностей.

Ответ:

Арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами. В этом пункте покажем, что неравенства, которым удовлетворяют элементы сходящихся последовательностей, в пределе переходят в соответствующие неравенства для пределов этих последовательностей.

Теорема . Если элементы сходящейся последовательности {x n x n ≥ b (x n ≤ b ), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b ).

Доказательство . Пусть все элементы x n , по крайней мере начиная с некоторого номера, удовлетворяют неравенству x n ≥ b . Требуется доказать неравенство a ≥ b . Предположим, что a < b . Поскольку a - предел последовательности {x n }, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |x n - a | < b - a . Это неравенство эквивалентно следующим двум неравенствам: -(b - a ) < x n - a < b - a . Используя правое из этих неравенств, получим x n < b , а это противоречит условию теоремы. Случай x n ≤ b рассматривается аналогично. Теорема доказана.

Замечание . Элементы сходящейся последовательности {x n } могут удовлетворять строгому неравенству x n > b , однако при этом предел a может оказаться равным b . Например, если , то x n > 0, однако

Следствие 1 . Если элементы x n и y n сходящихся последовательностей {x n } и {y n }, начиная с некоторого номера, удовлетворяют неравенству x n ≤ y n , то их пределы удовлетворяют такому же неравенству:

В самом деле, элементы последовательности {y n - x n } неотрицательны, а поэтому неотрицателен и ее предел

Отсюда следует, что

Следствие 2 . Если все элементы сходящейся последовательности {x n } находятся на сегменте [a , b ], то и ее предел c также находится на этом сегменте.

В самом деле, так как a ≤ x n ≤ b , то a ≤ c ≤ b .

Следующая теорема играет важную роль в различных приложениях.

Теорема . Пусть {x n } и {z n } - сходящиеся последовательности, имеющие общий предел a . Пусть, кроме того, начиная с некоторого номера, элементы последовательности {y n } удовлетворяют неравенствам x n ≤ y n ≤ z n . Тогда последовательность {y n } сходится и имеет предел a .

Доказательство . Нам достаточно доказать, что последовательность {y n - a } является бесконечно малой. Обозначим через N * номер, начиная с которого выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполняться также неравенства x n - a ≤ y n - a ≤ z n - a . Отсюда следует, что при n ≥ N * элементы последовательности {y n - a } удовлетворяют неравенству

|y n - a | ≤ max {|x n - a |, |z n - a |}.

Так как и , то для любого ε > 0 можно указать номера N 1 и N 2 такие, что при n ≥ N 1 |x n - a | < ε , а при n ≥ N 2 |z n - a | < ε . Пусть N = max{N * , N 1 , N 2 }. Начиная с этого номера, имеет место неравенство |y n - a | < ε . Итак, последовательность {y n - a } - бесконечно малая. Теорема доказана.

Еще по теме Предельный переход:

1. Переход к рыночной экономике связан с переходом к системе современного менеджмента, главным объектом которого становится организация (предприятие), а внутри нее - человек труда, работник.
2. Предельная величина (предельное значение экономического показателя)