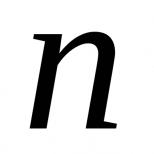Как найти частное решение ДУ приближённо с помощью ряда? Методы
Курсовая работа
по дисциплине: Высшая математика
на тему: Приближенные решения дифференциальных уравнений
Введение
При анализе режимов работы электроэнергетических объектов и разработке новых технологических процессов инженеру часто приходится сталкиваться с дифференциальными уравнениями, т.к. большая часть законов электротехники и теплотехники формулируется в виде дифференциальных уравнений. При этом нередко приходится иметь дело с уравнениями, общее решение которых не выражается в квадратурах. Например, общее решение очень простого уравнения нельзя записать в конечном виде через элементарные функции. Класс задач, для которых можно найти явное решение, весьма узок. В связи с интенсивным применением дифференциальных уравнений в качестве математических моделей широкого круга естественнонаучных задач и с появлением высокопроизводительных ЭВМ важное значение приобрели численные методы их решения. Численные методы - это алгоритмы вычисления приближенных значений искомого решения в точках конечного множества значений аргумента (узлах сетки). Решение при этом получается в виде таблицы. Рассмотрим два таких метода: метод Рунге-Кутта и вытекающий из него метод Эйлера.
Метод Рунге-Кутта. Рассматриваем задачу Коши для дифференциального уравнения первого порядка
решение которой находится на отрезке , h > 0. Считаем, что задача (1) имеет единственное решение у(х), определяемое на этом отрезке. Выбираем на отрезке [х0, x0 + H] сетку значений аргумента хд= х0 + nh , n=0,1,...,N; h= h/n. Разложим решение у (х) в ряд Тейлора в окрестности точки хn, полагая при этом уn=у(хn), у`= y`(xn) и т.д.
Подставим в разложение (2) значение х = xn+1, получая равенство
Стоящие в правой части равенства (3) производные можно найти, последовательно дифференцируя уравнение (1):
с учетом формул (5) равенство (3) можно записать последовательно в виде
Пренебрегая в правых частях формул (6) слагаемыми О(h2),О(h3), малыми при малых h, получаем соответственно формулы
Каждая из формул (7),(8),... позволяет по известному значению y0 решения задачи (1) в начальной точке xо последовательно вычислять приближенные значения этого решения в узлах сетки х1,х0,...,xn; в отличие от точных значений обозначим их
Формулу (8) и тем более, формулы с большим числом членов в практических расчетах не используют, так как если функция f(х,у) правой части имеет несложное выражение, то выражения (4) для ее производных могут оказаться громоздкими. Если функция f(х,у) известна лишь приближенно, то процесс вычислений по этим формулам усложняется еще и из-за необходимости использовать формулы численного, дифференцирования. Расчет приближенных значений уn задачи Коши (1) по формуле (7) называется методом Эйлера, или схемой ломаных. Геометрическая интерпретация этой схемы дана на рис.1, где изображено поле интегральных кривых.
Размещено на http://www.сайт/
При удалении от точки (хо,уо) ломаная Эйлера может заметно отклоняться от графика точного решения. Известна следующая оценка погрешности метода Эйлера. Пусть в D={(х,у): |х-хo |<а; |у-уо| Где С1
=(1+М) (еКН-1) При отсутствии ошибок округлений локальная погрешность метода Эйлера, т.е. погрешность на одном шаге h , возникающая за счет перемещения по касательной к интегральной кривой, проходящей через точку (хn,уn), а не по самой интегральной кривой, есть величина O(h2). Глобальная погрешность или, точнее, максимальная погрешность решения на сетке {х1,x2,...,хN} в целом равна O(h), как следует из неравенства (9). В связи с этим говорят, что метод Эйлера имеет первый порядок точности. С другой стороны в учебнике «Краткий курс математического анализа» А.Ф.Бермант, И.Г.Араманович, М. 1973 г этот метод описывается иначе. Известно, что уравнение задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке. Если взять последовательность точек х0, х1, х2,
…. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию. При подстановке заданных начальных условий (х0, у0
) в дифференциальное уравнение получаем угловой коэффициент касательной к интегральной кривой в начальной точке Заменив на отрезке интегральную кривую на касательную к ней, получаем значение Производя аналогичную операцию для отрезка , получаем: Если последовательность точек хi выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу: Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета. Суть метода состоит в том, что в формуле вместо значения берется среднее арифметическое значений f
(x
0,
y
0)
и f
(x
1,
y
1)
. Тогда уточненное значение: Затем находится значение производной в точке. Заменяя f
(x
0,
y
0)
средним арифметическим значений f
(x
0,
y
0)
и
, находят второе уточненное значение у1
. Затем третье: и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М1 ломаной Эйлера. Аналогичная операция производится для остальных значений у
. Подобное уточнение позволяет существенно повысить точность результата. Одним из методов, позволяющих для решения задачи Коши (1) строить вычислительные схемы более высоких порядков точности, является метод, предложенный Рунге и усовершенствованный Кутта и другими математиками. Схемы метода Рунге-Кутта удобны как, для расчетов на ЭВМ, так и для ручных расчетов. С основной идеей метода ознакомимся на примере построения вычислительных схем второго порядка точности. Воспользуемся теперь второй из формул (6) Покажем, что можно правильно передать члены ряда Тейлора, указанные в формуле (10), избежав дифференцирования, функция f(x,y), С этой целью полагаем где -некоторые постоянные По формуле Тейлора первого порядка находим Подставляя это выражение для значения в равенство (11) получаем Выбираем параметры так, чтобы правые части разложений (10) и (12) совпадали с точностью до слагаемых порядка О(h3). Для этого достаточно положить: Эта система трех уравнений с четырьмя неизвестными имеет бесконечно много решении. Выразим через остальные параметры: и подставим их в формулу (12), пренебрегая при этом слагаемыми О(h3). B результате получаем однопараметрическое семейство двучленных схем Локальная погрешность формулы (13) равна О(h3). Для максимальной погрешности на сетке выполняется оценка где С2 - некоторая постоянная, не зависящая от h. Вычислительная схема расчета приближенных значений решения задачи Коши (1) по формуле (13) называется схемой Рунге-Кутта второго порядка точности. Эти схемы нередко используются в практических вычислениях. При этом полагают, либо, либо. В первом случае получается схема особенно простого вида Для схема (13) имеет вид Методом Рунге-Кутта можно строить схемы различного порядка точности. Например, схема ломаных (7) есть схема Рунге-Кутта первого порядка точности, двучленные схемы (13) имеют второй порядок точности. Наибольшее распространение получили схемы четвертого порядка точности, при построении которых в записи ряда Тейлора (2) удерживаются все члены, включая h4. Приведем без вывода ту из них, которая записана в большинстве стандартных программ для ЭВМ: Для схемы (16) выполняется следующая оценка погрешности: если в прямоугольнике d существуют непрерывные частные производные четвертого порядка функции f
(x,у), то Схемы Рунге-Кутта более высокого порядка точности практически не употребляются, так как расчетные формулы становятся слишком громоздкими. Одним из важных достоинств метода Рунге-Кутта является простота алгоритма вычислений. Для начала вычислений достаточно выбрать сетку {хо, х1, ..., xN} и задать начальное значение у (хо) = уо. Далее вычисления производят последовательно по одним и тем же формулам. Это свойство схем метода Рунге-Кутта очень ценно при расчетах на ЭВМ, программирование расчетных формул метода не представляет труда. Выбор шага. Апостериорная оценка погрешности. Правило Рунге
Правильный выбор шага сетки h
является одним из главных практических вопросов, которые возникают при численном решении дифференциальных уравнений. Как получить требуемую точность? Если шаг выбран слишком большим, то значительной будет локальная погрешность и накопившаяся глобальная погрешность может быть недопустимо большой. Если же шаг слишком мал, то расчет потребует неоправданно много времени работы вычислителя или ЭВМ. При этом наблюдается следующий отрицательный эффект: суммарное действие ошибок округления, малых при выполнении каждой операции, может оказаться столь значительным, что полученный ответ становится бесполезным. Априорные оценки типа (9) мало полезны для получения информации о точности вычислений ввиду их сложности (особенно для схем высокого порядка); при этом они, как правило, во много раз превосходят фактическую ошибку расчета. Основным практическим приемом является апостериорная оценка погрешности. Для ее получения проводят вычисления на двух или более сгущающихся сетках и применяют так называемое правило Рунге, которое заключается в следующем. Пусть обозначает приближенное значение решения задача Коши (1) в точке х = x(h) = xo + nh, вычисленное по некоторой схеме Рунге-Кутта p-го порядка точности, а приближенное значение для y(x), вычисленное по той же схеме и в той же
точке, являющейся узлом более густой сетки с шагом h/2, так что. При некоторых предположениях относительно гладкости функции правой части f(x,y) погрешность схемы Рунге-Кутта р-го порядка точности имеет вид где С зависит от точки х, но не от h. Применяя формулу (17) для оценки погрешности на сетке с шагом h/2 , получаем Сохраняем в равенствах (17) и (18) только главную часть погрешности, пренебрегая слагаемыми и, и вычитаем почленно из первого равенства второе. В итоге приходим к приближенному равенству откуда определяем, что погрешность на сетке с меньшимшагом составляет частности, оценка (19) имеет вид: для схемы ломаных (7) для схемы (13) для схемы (16) Информацию о погрешности вычислений в виде (19) можно использовать для того, чтобы уточнить приближенные значения на сетке с меньшим шагом, внося в них поправки следующим образом. В точке, являющейся общим узлом двух сеток, полагаем в соответствии о формулами (18) и (19): дифференциальный уравнение точность погрешность Значения поправок, в узлах с нечетными номерами m=2n-1 находим, применяя линейную интерполяцию; Можно ожидать, что исправленные значения будут более точными, чем. Пример практического расчета
Используя метод Эйлера, а затем схему Рунге-Кутта второго порядка точности составить таблицу приближенных значений решения задачи Коши на отрезке с шагом h=0,2 и h=0,1. Результат округлить до 10-4. Оценить погрешность на сетке с шагом h=0,1 по методу Рунге. Сравнить полученные результаты с результатами вычислений по схеме четвертого порядка точности на сетке с шагом h=0,1. В таблицах 2 и 3: По методу Эйлера (табл.1) Таблица 1 h
=0,2 Таблица 2 Таблица приближенных значений по схеме Рунге-Кутта второго порядка точности шаг h
=0,1 Таблица 3 Оценим погрешность на сетке с шагом h
=0,1 по методу Рунге. В таблице 4: Таблица 4 Таблица приближенных значений по методу Рунге-Кутта четвертого порядка точности h
=0,1. Таблица 5 По результатам таблиц построим 4 графика yn
=
f
(xn
)
Как видно из графика более точные значения решения задачи Коши (полученные по схеме Рунге-Кутта второго и четвертого порядка точности с шагом h
=0,1 графики 2 и 3) лежат между менее точными значениями (полученные методом Эйлера и по схеме Рунге-Кутта второго порядка точности с шагом h
=0,2 графики 1 и 4) Литература
1. Методическое указание к лабораторной работе «Метод сеток. II. Решение задачи Коши для обыкновенного дифференциального уравнения первого порядка». Архангельск 1985 2. «Краткий курс математического анализа» А.Ф.Бермант, И.Г.Араманович, М. 1973 г. Хемминг Р.В., «Численные методы», «Наука». Основные методы Рунге-Кутта: построение класса расчетных формул. Расчетная формула метода Эйлера. Получение различных методов Рунге-Кутта с погрешностью второго порядка малости при произвольном задавании параметров. Особенности повышения порядка точности. реферат , добавлен 18.04.2015 Общая характеристика и особенности двух методов решения обычных дифференциальных уравнений – Эйлера первого порядка точности и Рунге-Кутта четвёртого порядка точности. Листинг программы для решения обычного дифференциального уравнения в Visual Basic. курсовая работа , добавлен 04.06.2010 Изучение методов Рунге-Кутты четвертого порядка с автоматическим выбором длины шага интегрирования для решения дифференциальных уравнений. Оценка погрешности и сходимость методов, оптимальный выбор шага. Листинг программы для ЭВМ, результаты, иллюстрации. курсовая работа , добавлен 14.09.2010 Численное решение уравнения методом Эйлера и Рунге-Кутта в Excel. Программа на языке Turbo Pascal. Блок-схема алгоритма. Метод Рунге-Кутта для дифференциального уравнения второго порядка. Модель типа "хищник-жертва" с учетом внутривидового взаимодействия. курсовая работа , добавлен 01.03.2012 Решение задачи Коши для дифференциального уравнения. Погрешность приближенных решений. Функция, реализующая явный метод Эйлера. Вычисление погрешности по правилу Рунге. Решение дифференциальных уравнений второго порядка. Условие устойчивости для матрицы. контрольная работа , добавлен 13.06.2012 Составление диагональной системы способом прогонки, нахождение решения задачи Коши для дифференциального уравнения на сетке методом Эйлера и классическим методом Рунге-Кутта. Построение кубического сплайна интерполирующей функции равномерного разбиения. практическая работа , добавлен 06.06.2011 Аналитическое и компьютерное исследования уравнения и модели Ван-дер-Поля. Сущность и особенности применения методов Эйлера и Рунге-Кутта 4 порядка. Сравнение точности метода Эйлера и Рунге-Кутта на одном графике, рисуя фазовые траектории из 1 точки. курсовая работа , добавлен 06.10.2012 Понятие, закономерности формирования и решения дифференциальных уравнений. Теорема о существовании и единственности решения задачи Коши. Существующие подходы и методы решения данной задачи, оценка погрешности полученных значений. Листинг программы. курсовая работа , добавлен 27.01.2014 Задачи Коши и методы их решения. Общие понятия, сходимость явных способов типа Рунге-Кутты, практическая оценка погрешности приближенного решения. Автоматический выбор шага интегрирования, анализ брюсселятора и метод Зонневельда для его расчета. курсовая работа , добавлен 03.11.2011 Дифференциальное уравнение первого порядка, разрешенное относительно производной. Применение рекуррентного соотношения. Техника применения метода Эйлера для численного решения уравнения первого порядка. Численные методы, пригодные для решения задачи Коши. Класс уравнений, для которых можно получить точное решение, то есть, аналитическую функцию, удовлетворяющую заданному дифференциальному уравнению и всем дополнительным условиям (задача Коши), очень узок. Чаще всего дифференциальные уравнения решаются приближенно. С одним из методов – итерационным – мы познакомились при доказательстве теоремы существования и единственности. 1. Приближение решения с помощью степенного ряда
. Представим, что мы должны решить задачу Коши для дифференциального уравнения -го порядка с начальным условием . Если функция в правой части уравнения разлагается в ряды по всем своим переменным, удобно искать решение дифференциального уравнения в окрестности точки в виде ряда Тейлора по степеням . Представим решение в виде . Из начальных условий и свойств коэффициентов ряда Тейлора следует, что все коэффициенты разложения вплоть до нам известны: остальные – неизвестные – коэффициенты обозначаются буквами и определяются сравнением коэффициентов при одинаковых степенях, находящихся в обеих частях дифференциального уравнения. П р и м е р. Решить следующую задачу Коши: , Искать решение будем в виде ряда по степеням . В соответствии с начальными условиями . Подставим хотя бы первые слагаемые рядов в уравнение: Перемножим входящие в правую часть сомножители: А теперь сравним свободные члены (они равны) и коэффициенты при , при и при : . Отсюда Мы могли бы и далее сравнивать коэффициенты при степенях в уравнении и получать значения других коэффициентов . Тем более применение программ MAXIMA упрощает этот процесс. В данном случае мы получили решение в виде ряда, первые члены которого известны: . Задачу Коши для системы уравнений можно решать подобным способом. 2. Метод Эйлера и его модификации
. Познакомимся с методом Эйлера численного решения задачи Коши для дифференциального уравнения первого порядка . Предположим, что мы должны решить задачу на отрезке . Разделим отрезок на равных частей, равных . Заменим на каждом отрезке , Мы здесь приравниваем отношение приращений функции и аргумента производной в точке, соответствующей началу отрезка разбиения: Очевидно, что такое приближение является тем менее точным, чем дальше мы отойдем от точки . Метод Эйлера является наиболее примитивным. Здесь интегральная кривая заменяется ломаной, состоящей из прямолинейных отрезков. Возможны его некоторые модификации, несколько улучшающие точность. Например, если брать постоянные значения в виде Наиболее распространенным численным методом решения указанной задачи Коши является метод Рунге-Кутта.
При решениидифференциального уравнения этим методом интегральная кривая заменяется ломаной, состоящей из кусков парабол. Метод Рунге-Кутта встроен в пакет программ MAXIMA. Например, мы хотим решить дифференциальное уравнение с начальным условием . При этом мы задаем отрезок , на котором хотим получить численное решение и шаг разбиения этого отрезка, равный 0.05. Мы должны ввести команду load(dynamics); rk(y^2+x,y,0.3,);
После того, как мы нажмем клавиши Shift+Enter, получим данные [,,,,,,,,,,,,,,,,,,,,]. Это означает, что мы получили узловые значения решения: y
(0.05)= 0.30583128660202,…, y
(0.4)= 0.42905553899765,….. Приближенное решение дифференциальных уравнений высших порядков
сводятся к решению систем уравнений первого порядка. Например, требуется решить дифференциальное уравнение с начальными условиями Для получения решения методом Рунге-Кутта вводим команду load(dynamics); rk(, , , ).
Мы получим значения в узлах: [,,,,,,,,,,,,,,,,[ 1.6,0.55276102463945,-9.157645341403534],, Это означает, что, например, y(0.5)= 1.227625229955781, z(0.5)= 0.80905909503231. 3. Графический метод
. Этим методом можно решать дифференциальные уравнения первого порядка вида . Если нам необходимо построить интегральные кривые, которые являются графиками решений приведенного уравнения, в какой-то части плоскости , мы каждой точке этой области ставим в соответствие значение , которое совпадает с тангенсом угла наклона касательной к интегральной кривой, проходящей через точку . Зная точку и направление движения по кривой из этой точки, мы переходим к близкой точке, в которой также определяем направление движения,…. Так, двигаясь от точки к точке, мы построим соответствующую интегральную кривую, то есть, решим задачу Коши . Реальное построение решения таким методом было бы очень сложным без применения компьютерной техники. MAXIMA содержит программу построения графических решений. Если мы введем load(plotdf); plotdf(f(x,y),,)
, на экране появится прямоугольник , в точках которого указаны направления касательных к интегральным кривым, проходящим через эти точки. Если щелкнуть курсором по выбранной точке на плоскости, компьютер нарисует интегральную кривую, проходящую через соответствующую точку. Например, мы хотим построить интегральную кривую уравнения Введем load(plotdf); plotdf((5-x^2)/(2*x*y-y^2),,);
и нажмем Shift+Enter. Мы получим выбранный прямоугольник с указанием направлений из точек прямоугольника. Теперь щелкнем по точке (11,2) , и нарисуется соответствующая интегральная кривая. Рассмотрим задачу Коши (5.2), (5.6) для дифференциального уравнения первого порядка: найти решение уравнения y"=f(x,y), удовлетворяющее условию y(x 0)=y 0 . Пусть y(x)- решение поставленной задачи Коши. Подставив это решение в уравнение (5.2), получим тождество y"(x) ≡ f(x,y(x)). Интегрируя это тождество по x, получаем
или, что тоже самое, Таким образом, мы показали, что всякое решение задачи Коши (5.2), (5.6) есть решение интегрального уравнения (5.15). С другой стороны, если y(x)- решение интегрального уравнения (5.15), то дифференцируя (5.15) по x, получаем, что y(x)- решение задачи Коши (5.2), (5.6). Решение интегрального уравнения (5.15) будем искать с помощью метода последовательных приближений. Положим y 0 (x)=y 0 ,
Если оператор сжимающий , то последовательные приближения (5.16) сходятся к решению интегрального уравнения (5.15), а, следовательно и дифференциального уравнения y" = f(x,y), удовлетворяющего условию y(x 0) = y 0 . Желающие могут познакомиться с доказательством сжимаемости оператора (5.17) в . Пример №1
. Найдём с помощью метода последовательных приближений решение уравнения y" = y, удовлетворяющее условию y(0)=1. Подставляя y(0)=1 в (5.16), получаем y 0 =1,
С другой стороны, решая исходную задачу Коши, имеем y = e x . Таким образом, нами получено разложение функции e x в ряд Тейлора в нуле (ряд Маклорена). Перейдём теперь к изложению численного метода Эйлера решения задачи Коши (5.2), (5.6). Разобьём отрезок , на котором мы ищем решение, на части точками x 0 = a y i +1 = y i + h·f(x i , y i), (5.17) Соотношение (5.17) является расчётной формулой метода Эйлера численного решения задачи Коши (5.2), (5.6). Вычислив y i , i = 0,1,..,n получим таблицу значений решения в точках x i , i = 0,1,..,n Для оценки погрешности на одном шаге сетки в методе Эйлера разложим точное решение y(x) по формуле Тейлора в окрестности точки xi
до членов второго порядка малости y(x i +1)=y(x i +h)=y(x i)+y"(x i)h+o(h 2)=y i +hf(x i ,y i)+o(h 2). Сравнивая с (5.17) видим, что погрешность формулы (5.17) равна o(h 2). К сожалению, метод Эйлера накапливает ошибку от шага к шагу. Поэтому на практике пользуются либо модификациями метода Эйлера, например методом прогноза и коррекции , либо другими методами, в частности методом Рунге-Кутта . С дифференциальными уравнениями в частных производных и интегральными уравнениями приходится встречаться в самых разнообразных областях естествознания, причем получить их решение в явном виде, в виде конечной формулы, удается только в самых простейших случаях. В связи с этим особое значение приобретают приближенные методы решения различных задач для дифференциальных уравнений в частных производных, систем дифференциальных уравнений в частных производных и интегральных уравнений или, как часто говорят, задач математической физики. В настоящей главе мы и рассмотрим некоторые, наиболее распространенные методы решения задач математической физики. При этом мы ограничимся в основном методами решения задач для линейных дифференциальных уравнений в частных производных второго порядка с двумя независимыми переменными и линейными интегральными уравнениями, в которых искомая функция зависит только от одного независимого переменного. Изложение методов для случая произвольного числа переменных было бы связано с очень громоздкими записями, в то время как основные идеи методов, а также возникающие при их реализации трудности хорошо усматриваются в простейших случаях. Что касается нелинейных уравнений, то хотя отдельные задачи для нелинейных уравнений и были разрешены, однако общая теория приближенных методов для нелинейных уравнений все еще отсутствует. В последнее время численным методам решения задач для нелинейных уравнений уделяется много внимания, но их разработка еще не достигла такого состояния, при котором их можно было бы включить в учебное пособие. Как и в случае обыкновенных дифференциальных уравнений, приближенные методы решения различных задач для дифференциальных уравнений в частных производных можно разбить на две группы: 1) методы, в которых приближенное решение получается в аналитической форме, например в виде отрезка некоторого ряда, и 2) методы, с помощью которых можно получить таблицу приближенных значений искомого решения в некоторых точках рассматриваемой области, - численные методы. К первой группе относится прежде всего метод Фурье решения краевых задач для дифференциальных уравнений в частных производных, при применении которого точное решение получается в виде некоторого ряда, а за приближенное решение может быть принята сумма некоторого числа первых его членов. Метод Фурье решения классических задач математической физики подробно излагается в курсе математической физики, и мы на нем совсем не будем останавливаться. Из методов первой группы мы рассмотрим лишь вариационные методы решения краевых задач для уравнений в частных производных и близкий к ним метод Галеркина. Наиболее широко распространенным методом численного решения задач для дифференциальных уравнений в частных производных является метод сеток, или метод конечных разностей, а также метод характеристик решения уравнений и систем уравнений гиперболического типа, который в сущности также является конечноразностным методом, только в этом методе дифференциальное уравнение в частных производных или система таких уравнений предварительно сводится к эквивалентной ей системе обыкновенных дифференциальных уравнений, которая и решается разностным методом. Описанию метода сеток для решения некоторых задач математической физики в основном и посвящена эта глава. Особое место занимает метод прямых, который в зависимости от способа его реализации может быть отнесен как к той, так и к другой группе методов. В этом методе ищется приближенно решение дифференциального уравнения в частных производных вдоль некоторого семейства прямых. При этом вместо дифференциального уравнения в частных производных получается система обыкновенных дифференциальных уравнений. Если эта система решается в конечном виде, то мы получаем приближенное решение дифференциального уравнения в частных производных в виде системы функций, приближенно представляющих искомое решение вдоль рассматриваемых прямых. Если же система обыкновенных дифференциальных уравнений решается численными методами, то и приближенное решение уравнения в частных производных получается в виде таблицы, и в этом случае этот метод можно отнести к группе численных методов. В последнем параграфе главы изложены методы приближенного решения линейных интегральных уравнений типа Фредгольма и Вольтерра. В силу значительных трудностей, возникающих при приближенном решении дифференциальных уравнений в частных производных мы ограничимся при изложении из педагогических соображений только простейшими уравнениями и простейшими задачами для них, причем во многих случаях не приводятся доказательства сходимости, а также оценки погрешностей, если даже они существуют. Это отнюдь не означает, что описанные методы неприменимы для решения других более сложных задач.
Подобные документы

![]() .
.
![]() .
.![]() , решение дифференциального уравнения линейной функцией . При этом имеем узловые значения решения:
, решение дифференциального уравнения линейной функцией . При этом имеем узловые значения решения: ![]() .
.![]() на отрезке с шагом 0.1 при начальных условиях
на отрезке с шагом 0.1 при начальных условиях ![]() . Введем новую функцию . Теперь уравнение запишется в виде системы
. Введем новую функцию . Теперь уравнение запишется в виде системы 
![]() .
. , расположенную в прямоугольнике
, расположенную в прямоугольнике ![]() и проходящую через точку (11,2) .
и проходящую через точку (11,2) .
 . (5.15)
. (5.15) . (5.16)
. (5.16) - (5.17)
- (5.17)
 …,
…,![]()
![]() в уравнении (5.2), получаем
в уравнении (5.2), получаем ![]() , или, что то же самое,
, или, что то же самое,